
10.定义函数 ,若存在常数C,对任意的
,若存在常数C,对任意的 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的几何平均数为C.已知
在D上的几何平均数为C.已知 ,则函数
,则函数 在
在 上的几何平均数为( )
上的几何平均数为( )
(A) (B)
(B) (C)
(C) (D)
(D)
9. 下列命题中正确的是 ( )
(A) 设f (x) = sin(2x+ ),
则"xÎ
),
则"xÎ ,必有f(x) < f (x + 0.1)
,必有f(x) < f (x + 0.1)
(B) $x0ÎR。便得
(C) 设f (x) = cos(x +  ),
则函数y = f (x +
),
则函数y = f (x + )
是奇函数
)
是奇函数
(D) 设f ( x ) = 2sin2x,则f (x + ) = 2sin(2x +  )
)
8.已知 则
则 ( )
( )
(A)–180 (B)180 (C)45 (D) –45
7.设等差数列 的前
的前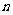 项和为
项和为 ,则
,则 是
是 的( )
的( )
(A)充分但不必要条件 (B)必要但不充分条件
(C)充要条件 (D)既不充分也不必要条件
6.设不等式组 所表示的区域为
所表示的区域为 ,现在区域
,现在区域 中任意丢进一个粒子,则该粒子落在直线
中任意丢进一个粒子,则该粒子落在直线 下方的概率为 ( )
下方的概率为 ( )
(A)  (B)
(B)  (C)
(C)  (D)
(D) 
4.向量a = (1,2),b = (x,1),c = 2a + b,d = 2a-b,若c//d,则实数x的值等于( ).
(A)  (B)
(B) (C)
(C) (D)
(D)
5执行如图的程序框图,如果输入 ,则输出的
,则输出的 ( )
( )
(A)  (B)
(B)  (C)
(C)  (D)
(D) 
3. 函数 的定义域是 ( )
的定义域是 ( )
(A) (B)
(B) (C)
(C) (D)
(D)
2.复数 的虚部是 ( )
的虚部是 ( )
 (第5题) |
(A) -1 (B) 1 (C)i (D)3
1.设集合 A∪(CUB)=( )
A∪(CUB)=( )
(A){1} (B){1,2} (C) {2} (D){0,1,2}
22. (本题15分)
由题意得 .
.
(I) 4分
4分
(II)讨论:(1)当 时,
时,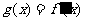 的零点
的零点 ;
;
(2)当 时,
时, 的零点
的零点 ,不合题意; 4分
,不合题意; 4分
(3)当 时,
时,
(4)当 时,
时,
综上所述, 7分
7分
(II)另解: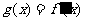 在区间
在区间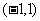 上存在零点,等价于
上存在零点,等价于 在区间
在区间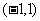 上有解,
上有解,
也等价于直线 与曲线
与曲线 有公共点,
有公共点,
作图可得  . 7分
. 7分
或者:又等价于当 时
,求值域:
时
,求值域: . 7分
. 7分
|
|||||
 |
|||||
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com