
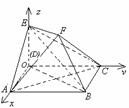
19.解法一: (1)证:记AC与BD的交点为O,连接EO,则可证BF∥EO,又
(1)证:记AC与BD的交点为O,连接EO,则可证BF∥EO,又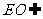 面ACE,
面ACE,
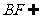 面ACE,故BF∥平面ACE;………………………3分
面ACE,故BF∥平面ACE;………………………3分
(2)解:过点O作OG⊥AF于点G,连接GB,则可证∠OGB为二面角B-AF-C的平面角.
 在Rt△FOA中,可求得OG=
在Rt△FOA中,可求得OG=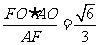 ,又OB=
,又OB=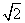 ,故
,故
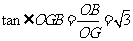 ,
,
∴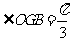 ,即二面角B-AF-C的大小为
,即二面角B-AF-C的大小为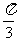 ;………………8分
;………………8分
(3)点F到平面ACE的距离等于点B到平面ACE的距离,也等于点
D到平面ACE的距离,该距离就是Rt△EDO斜边上的高,
即 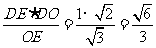 .∴点
.∴点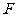 到平面
到平面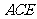 的距离为
的距离为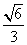 …………………12分
…………………12分
 解法二:(1)同解法一…………………3分
解法二:(1)同解法一…………………3分
(2)建立空间坐标率如图所示:则A(2,0,0),C(0,2,0)
E(0,0,1),B(2,2,0),F(1,1,1);
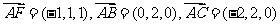
设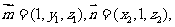 分别是平面ABF和平面ACF的一个法向量
分别是平面ABF和平面ACF的一个法向量
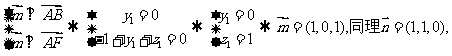
设二面角B-AF-C的大小为α,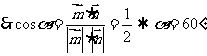 …………………8分
…………………8分
(3)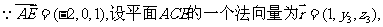 由
由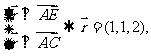
设F到平面ACE的距离为d,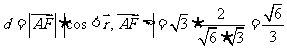 ………………12分
………………12分
18.解:(1)记事件 “该应聘者参加前4个环节的考核而入围”,则
“该应聘者参加前4个环节的考核而入围”,则
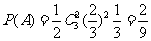
∴该应聘者参加完前4个环节的考核且只参加前4个环节的考核而入围的概率是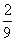 ……3分
……3分
(2)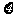 的可能取值为3,4,5
的可能取值为3,4,5
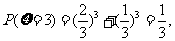 …………5分
…………5分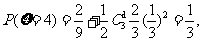 …………7分
…………7分
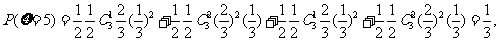 ……9分
……9分
∴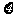 分布列为
分布列为
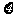 |
3 |
4 |
5 |
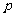 |
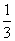 |
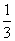 |
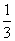 |
……10分
∴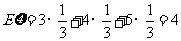 …………………………12分
…………………………12分
17.解:(1) 因为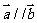 ,所以
,所以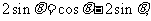
于是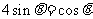 ,故
,故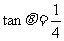 …………………………6分
…………………………6分
(2)由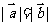 知,
知,
所以
从而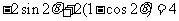 ,即
,即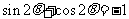 ,……………………8分
,……………………8分
于是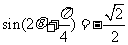 .又由
.又由 知,
知,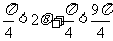 ,
,
所以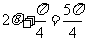 ,或
,或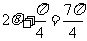 .因此
.因此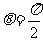 ,或
,或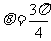 …………………12分
…………………12分
16.(1)(2)(3)
15.
14.3
13.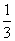
ABAC DCAD BADB
24、(本小题满分10分)选修4-5:不等式选讲
解不等式 .
.
23、(本小题满分10分)选修4-4:坐标系与参数方程
设过原点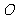 的直线与圆C:
的直线与圆C: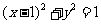 的一个交点为
的一个交点为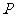 ,点
,点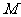 为线段
为线段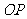 的中点。
的中点。
(1)求圆C的极坐标方程
(2)求点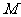 轨迹的极坐标方程,并说明它是什么曲线.
轨迹的极坐标方程,并说明它是什么曲线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com