
1.复数 的共轭复数是
的共轭复数是
A. B.
B.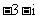 C.
C.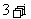 D.
D.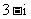
21.(本小题满分14分)
已知数列 满足对任意的
满足对任意的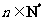 ,都有
,都有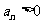 ,且
,且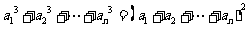 .
.
(1)求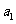 ,
,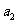 的值;
的值;
(2)求数列 的通项公式
的通项公式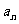 ;
;
(3)设数列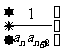 的前
的前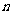 项和为
项和为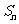 ,不等式
,不等式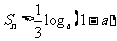 对任意的正整数
对任意的正整数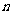 恒成立,求实
恒成立,求实
数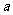 的取值范围.
的取值范围.
2010年广州市普通高中毕业班综合测试(一)
20.(本小题满分14分)
已知函数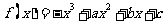 在
在 上是减函数,在
上是减函数,在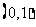 上是增函数,函数
上是增函数,函数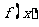 在
在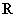 上有三个零点,且1是其中一个零点.
上有三个零点,且1是其中一个零点.
(1)求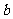 的值;
的值;
(2)求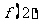 的取值范围;
的取值范围;
(3)试探究直线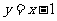 与函数
与函数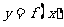 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.
19.(本小题满分14分)
已知动点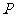 到定点
到定点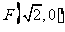 的距离与点
的距离与点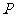 到定直线
到定直线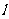 :
: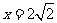 的距离之比为
的距离之比为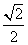 .
.
(1)求动点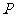 的轨迹
的轨迹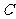 的方程;
的方程;
(2)设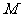 、
、 是直线
是直线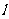 上的两个点,点
上的两个点,点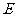 与点
与点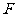 关于原点
关于原点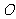 对称,若
对称,若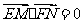 ,求
,求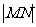 的最小值.
的最小值.
18.(本小题满分12分)
已知直线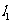 :
: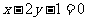 ,直线
,直线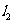 :
: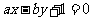 ,其中
,其中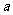 ,
,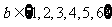 .
.
(1)求直线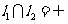 的概率;
的概率;
(2)求直线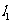 与
与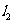 的交点位于第一象限的概率.
的交点位于第一象限的概率.
17. (本小题满分14分)
(本小题满分14分)
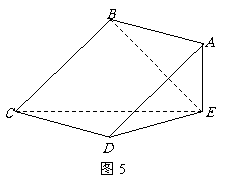
如图6,正方形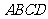 所在平面与三角形
所在平面与三角形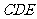 所在平面相交于
所在平面相交于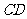 ,
,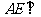 平面
平面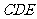 ,且
,且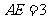 ,
,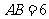 .
.
(1)求证: 平面
平面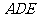 ;
;
(2)求凸多面体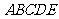 的体积.
的体积.
16.(本小题满分12分)
已知函数 (其中
(其中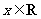 ,
,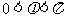 ).
).
(1)求函数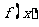 的最小正周期;
的最小正周期;
(2)若点 在函数
在函数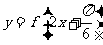 的图像上,求
的图像上,求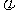 的值.
的值.
(一)必做题(11-13题)
11.在等比数列 中,
中,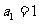 ,公比
,公比 ,若
,若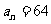 ,则
,则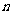 的值
的值
为 .
12.某算法的程序框如图4所示,若输出结果为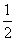 ,则输入的实数
,则输入的实数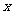
的值是________.
(注:框图中的赋值符号“=”也可以写成 “←”“:=”)
13.在△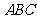 中,三边
中,三边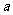 、
、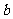 、
、 所对的角分别为
所对的角分别为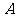 、
、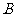 、
、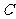 ,
,
若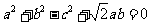 ,则角
,则角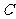 的大小为
.
的大小为
.
 (二)选做题(14-15题,考生只能从中选做一题)
(二)选做题(14-15题,考生只能从中选做一题)
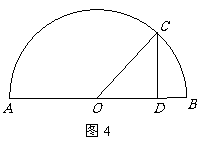
14.(几何证明选讲选做题)如图5,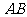 是半圆
是半圆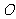 的直径,点
的直径,点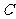 在
在
半圆上,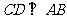 ,垂足为
,垂足为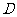 ,且
,且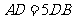 ,设
,设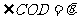 ,
,
则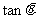 的值为 .
的值为 .
15.(坐标系与参数方程选做题)在极坐标系中,已知两点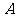 、
、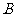 的极坐标分别为
的极坐标分别为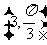 ,
, ,则△
,则△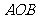 (其中
(其中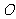 为极点)的面积为 .
为极点)的面积为 .
10.如图3所示的三角形数阵叫“莱布尼兹调和三角形”,
它们是由整数的倒数组成的,第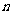 行有
行有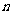 个数且两端
个数且两端
的数均为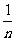
 ,每个数是它下一行左右相邻两数
,每个数是它下一行左右相邻两数
的和,如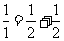 ,
, ,
, ,…,
,…,
则第7行第4个数(从左往右数)为
A.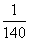 B.
B.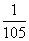
C.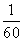 D.
D.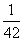
9.已知函数 若
若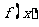 在
在 上单调递增,则实数
上单调递增,则实数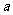 的取值范围为
的取值范围为
 A.
A.  B.
B. 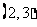 C.
C. 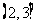 D.
D. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com