
22. Michelle Obama, ________ as the First Lady of the United States, presents to the world a new image of African-American woman.
A. having known B. known C. to be known D. knowing
20. 已知二次函数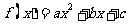 和“伪二次函数”
和“伪二次函数”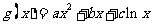 (
(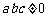 ),
),
(1)证明:只要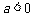 ,无论
,无论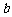 取何值,函数
取何值,函数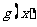 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(2)在同一函数图像上任意取不同两点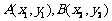 ,线段
,线段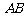 中点为
中点为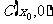 ,记直线
,记直线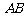 的斜率为
的斜率为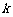 ,
,
1对于二次函数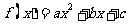 ,求证:
,求证: ;
;
2对于“伪二次函数”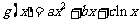 ,是否有1同样的性质?证明你的结论.
,是否有1同样的性质?证明你的结论.
19.(本小题满分16分)
已知函数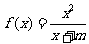 的图像经过点
的图像经过点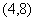 .
.
(1)求该函数的解析式;
(2)数列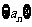 中,若
中,若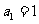 ,
,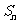
 为数列
为数列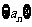 的前
的前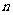 项和,且满足
项和,且满足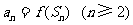 ,
,
证明数列 成等差数列,并求数列
成等差数列,并求数列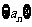 的通项公式;
的通项公式;
(3)另有一新数列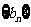 ,若将数列
,若将数列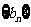 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成
如下数表:
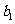
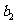
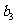
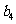

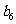
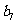
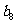
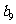
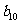
…………
记表中的第一列数 构成的数列即为数列
构成的数列即为数列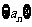 ,上表中,若从第三行起,第一行中的
,上表中,若从第三行起,第一行中的 数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
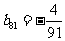 时,求上表中第
时,求上表中第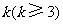 行所有项的和.
行所有项的和.
18.(本小题满分15分)
要制作一个由同底圆锥和圆柱组 成的储油罐(如图),设计要求:圆
成的储油罐(如图),设计要求:圆 锥和圆柱的总高度和圆柱底面半径相等,都为
锥和圆柱的总高度和圆柱底面半径相等,都为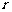 米.市场上,圆柱侧面用料单价为每平方米
米.市场上,圆柱侧面用料单价为每平方米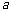 元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为
元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为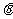 (弧度),总费用为
(弧度),总费用为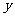 (元).
(元).
(1)写出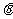 的取值范围;
的取值范围;
(2)将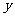 表示成
表示成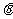 的函数关系式;
的函数关系式;
 (3)当
(3)当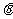 为何值时,总费用
为何值时,总费用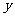 最小?
最小?
17.(本小题满分15分)
已知圆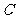 通过不同的三点
通过不同的三点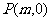 、
、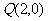 、
、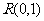 ,且
,且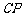 的斜率为
的斜率为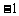 .
.
(1)试求
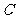 的方程;
的方程;
(2)过原点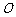 作两条互相垂直的直线
作两条互相垂直的直线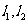 ,
,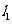 交
交
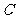 于
于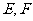 两点,
两点,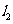 交
交
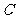 于
于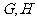 两点,求四边形
两点,求四边形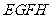 面积的最大值.
面积的最大值.
16.(本小题满分14分)
如图,多面体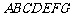 中,
中,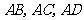 两两垂直,平面
两两垂直,平面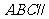 平面
平面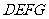 ,
,
平面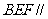 平面
平面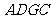 ,
,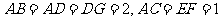 .
.
(1)证明四边形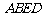 是正方形;
是正方形;
(2)判断点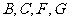 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?
 (3)连结
(3)连结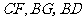 ,求证:
,求证: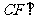 平面
平面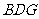 .
.
15.(本小题满分14分)
在△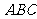 中,角
中,角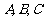 的对边分别为
的对边分别为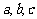 ,且满足
,且满足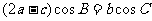 .
.
(1)求角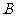 的大小;
的大小;
|
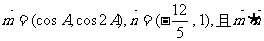 取最小值时,求
取最小值时,求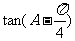 值.
值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com