
1、国家实行强有力的宏观调控。社会主义市场经济坚持公有制为主体,国家能够集中力量办大事;各地区和各有关部门要密切配合,形成合力,进一步完善应急预案,把各项抗旱救灾措施落到实处,一手抓抗旱救灾,一手抓经济社会发展,努力实现今年经济社会发展的各项目标,体现了社会主义制度的优越性。
(17) (本小题满分l0分)
已知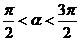 ,A、B、C在同一个平面直角坐标系中的坐标分别为
,A、B、C在同一个平面直角坐标系中的坐标分别为
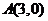 、
、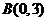 、
、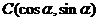 。
。
(I)若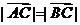 ,求角
,求角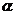 的值;
的值;
(II)当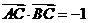 时,求
时,求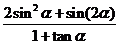 的值。
的值。
(18) (本小题满分12分)
在由正数组成的数列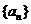 中,
中,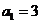 ,
,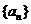 的前
的前 项和为
项和为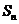 ,对任何正整数
,对任何正整数 ,等式
,等式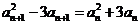 都成立。在等比数列
都成立。在等比数列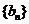 中,
中,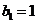 ,
,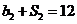 ,数列
,数列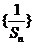 的前
的前 项和为
项和为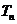 。
。
(I) 求数列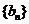 的通项公式;
的通项公式;
(II) 证明: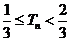 。
。
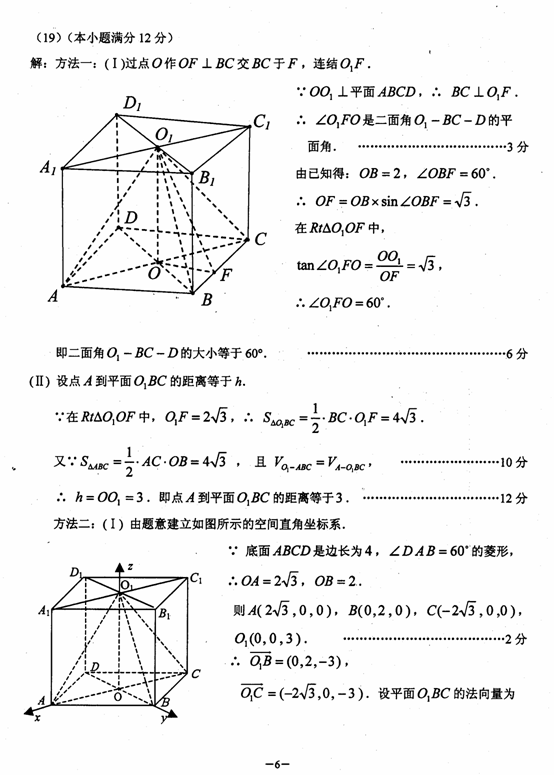
(19) (本小题满分12分)
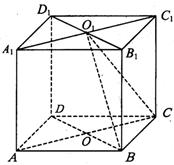 如图,直四棱柱
如图,直四棱柱 -
-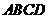 的高为3,底面是边长为4,且∠DAB=60°的菱形,
的高为3,底面是边长为4,且∠DAB=60°的菱形,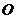 是
是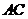 与
与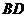 的交点,
的交点,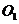 是
是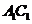 与
与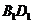 的交点。
的交点。
(I) 求二面角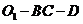 的大小;
的大小;
(II) 求点 到平面
到平面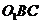 的距离。
的距离。
(20) (本小题满分12分)
一个盒子内装有八张卡片,每张卡片上面分别写着下列函数中的一个: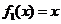 ,
,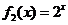 ,
,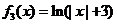 ,
,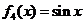 ,
,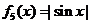 ,
,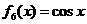 ,
,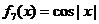 ,
,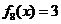 ,而且不同卡片上面写着的函数互不相同,每张卡片被取出的概率相等。
,而且不同卡片上面写着的函数互不相同,每张卡片被取出的概率相等。
(I) 如果从盒子中一次随机取出两张卡片,并且将取出的两张卡片上的函数相加得到一个新函数,求所得新函数是奇函数的概率;
(II) 现从盒子中一次随机取出一张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的函数是偶函数则停止取出卡片,否则继续取出卡片。设取出卡片3次才停止抽出卡片活动的概率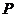 。
。
(21) (本小题满分12分)
已知焦点在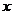 轴上的椭圆
轴上的椭圆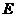 的中心是原点
的中心是原点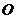 ,离心率等于
,离心率等于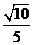 ,椭圆
,椭圆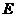 的右焦点
的右焦点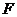 到椭圆
到椭圆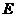 的右准线的距离等于
的右准线的距离等于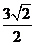 ,经过点
,经过点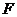 且斜率等于1的直线
且斜率等于1的直线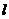 交椭圆
交椭圆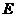 于
于 、
、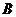 两点,
两点,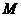 为线段
为线段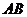 的中点,射线
的中点,射线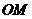 交椭圆
交椭圆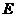 于
于 点。
点。
(I) 求椭圆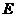 的方程。
的方程。
(II) 证明: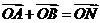 。
。
(22) (本小题满分12分)
己知常数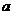 、
、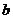 都是实数,
都是实数,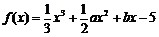 ,直线
,直线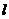 的方程为
的方程为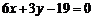 。
。
(I) 如果 在实数集
在实数集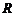 上是单调函数,求
上是单调函数,求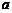 、
、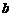 满足的条件;
满足的条件;
(II) 设点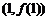 、
、 是
是 的两个极值点,问:
的两个极值点,问: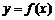 的图象上是否存在与直线
的图象上是否存在与直线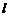 平行的切线?如果存在,求出直线
平行的切线?如果存在,求出直线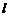 平行的切线的方程;如果不存在,请说明理由。
平行的切线的方程;如果不存在,请说明理由。





(13)函数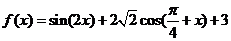 的最小值是 。
的最小值是 。
(14)在数列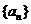 中,
中,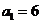 ,
,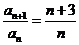 ,那么
,那么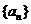 的通项公式是
。
的通项公式是
。
(15)若A、B两点在半径为2厘米的球面上,且AB=2厘米,设A、B两点在此球上的球面
距离为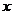 厘米,则
厘米,则 。
。
(16)已知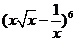 的二项展开式中的第5项的值等于
的二项展开式中的第5项的值等于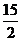 ,则
,则 。
。
(1)已知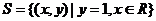 ,
,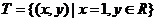 ,则
,则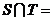
(A) 空集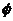 (B)
(B)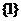 (C)
(1, 1) (D)
{(1, 1)}
(C)
(1, 1) (D)
{(1, 1)}
(2)为了了解甲、乙、丙三所学校高三数学模拟考试的情况,现采取分层抽样方法从甲校的1260份高三数学模拟试卷、乙校的720份高三数学模拟试卷、丙校的900份高三数学模拟试卷中抽取试卷进行调研。如果从丙校的900份试卷中抽取了50份试卷,那么这次调研一共抽查的试卷份数为
(A) 150 (B) 160 (C) 200 (D) 230
(3)已知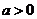 ,
,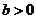 ,如果不等式
,如果不等式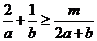 恒成立,那么
恒成立,那么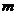 的最大值等于
的最大值等于
(A) 10 (B) 9 (C) 8 (D) 7
(4)已知数列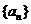 的前
的前 项和为
项和为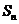 ,如果
,如果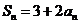 对任何正整数
对任何正整数 都成立,那么数列
都成立,那么数列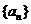
(A) 是等比数列但不是等差数列 (B) 是等差数列但不是等比数列
(C) 既是等差数列又是等比数列 (D) 既不是等差数列也不是等比数列
(5)已知减函数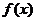 的定义域是实数集
的定义域是实数集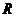 ,
,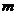 、
、 都是实数。如果不等式
都是实数。如果不等式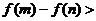
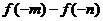 成立,那么下列不等式成立的是
成立,那么下列不等式成立的是
(A) 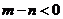 (B)
(B)
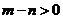
(C) 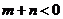 (D)
(D)
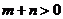
(6)在一次教师联欢会上,到会的女教师比男教师多12人,从到会教师中随机挑选一人表演
节目。如果每位教师被选到的概率相等,而且选到男教师的概率为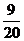 ,那么参加这次联
,那么参加这次联
欢会的教师共有
(A) 360人 (B) 240人 (C) 144人 (D) 120人
(7)已知双曲线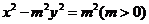 的一条渐近线与直线
的一条渐近线与直线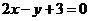 垂直,则该双曲
垂直,则该双曲
线的准线方程是
(A)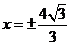 (B)
(B)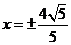
(C)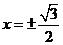 (D)
(D)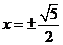
(8)在△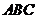 中,三内角
中,三内角 、
、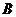 、
、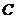 所对的边分别为
所对的边分别为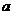 、
、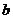 、
、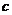 ,如果
,如果 ,
,
那么
(A) 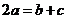 (B)
(B)
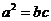
(C) 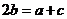 (D)
(D)
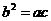
(9)下列函数中,最小正周期为2的函数是
(A)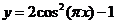 (B)
(B)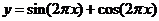
(C)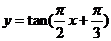 (D)
(D)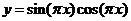
(10)已知抛物线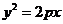 与直线
与直线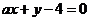 相交于A、B两点,其中点A的坐标是(1,2)。
相交于A、B两点,其中点A的坐标是(1,2)。
若抛物线的焦点为F,那么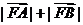 等于
等于
(A) 5 (B)
6 (C)
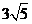 (D)
7
(D)
7
(11)已知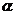 、
、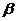 是两个不同的平面,
是两个不同的平面,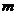 、
、 是两条不同的直线,给出下列命题:
是两条不同的直线,给出下列命题:
①若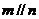 ,
,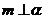 ,则
,则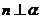 ; ②若
; ②若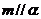 ,
,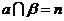 ,则
,则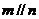 ;
;
③若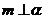 ,
,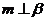 ,则
,则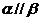 ; ④若
; ④若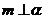 ,
,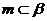 ,则
,则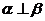 .
.
不正确的命题共有
(A) 1个 (B) 2个
(C) 3个 (D) 4个
(12)已知A(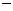 2,0)、B(0,2),实数
2,0)、B(0,2),实数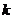 是常数,M、N是圆
是常数,M、N是圆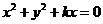 上的两个不同点,
上的两个不同点,
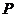 是圆
是圆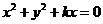 上的动点,如果M、N关于直线
上的动点,如果M、N关于直线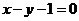 对称,那么△PAB
对称,那么△PAB
的面积的最大值等于
(A)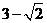 (B)
4
(B)
4
(C)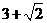 (D)
6
(D)
6
2010年云南省第一次高中毕业生复习统-检测
文科数学
第II卷(非选择题,共90分)
注意摹项:
本卷共3页,10小题,用黑色碳素笔将答案答在答题卡上。答在试卷上的答案无效。
23.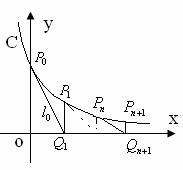 (本小题14分)如图,过曲线C:
(本小题14分)如图,过曲线C: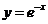 上一点
上一点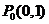 做曲线C的切线
做曲线C的切线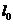 交x轴于
交x轴于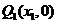 点,又过
点,又过 做x轴的垂线交曲线C于
做x轴的垂线交曲线C于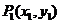 点,然后再过
点,然后再过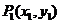 做曲线C的切线
做曲线C的切线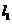 交x轴于
交x轴于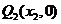 ,又过
,又过 做x轴的垂线交曲线C于
做x轴的垂线交曲线C于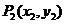 ,
,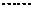 ,以此类推,过点
,以此类推,过点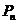 的切线
的切线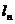 与x轴相交于点
与x轴相交于点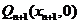 ,再过点
,再过点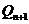 做x轴的垂线交曲线C于点
做x轴的垂线交曲线C于点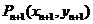 (n=1,2,3,…).
(n=1,2,3,…).
(1)求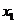 、
、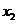 及数列
及数列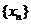 的通项公式;
的通项公式;
(2)设曲线C与切线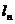 及垂线
及垂线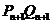 所围成的图形面积为
所围成的图形面积为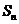 ,求
,求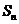 的表达式;
的表达式;
(3)若数列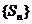 的前n项之和为
的前n项之和为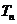 ,求证:
,求证: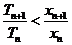
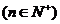 .
.
西工大附中高2010届第一次摸拟考试
22、(本小题13分)已知椭圆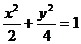 两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足
两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足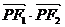 =1,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
=1,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
(1)求P点坐标; (2)求直线AB的斜率;
(3)求△PAB面积的最大值.
21.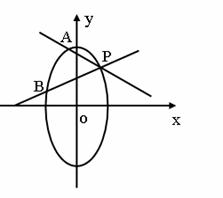 (本小题12分)已知函数
(本小题12分)已知函数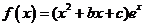 在点
在点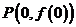 处的切线方程为
处的切线方程为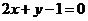 .
.
(1)求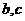 的值;(2)求函数
的值;(2)求函数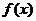 的单调区间;
的单调区间;
(3)若方程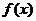 =m恰有两个不等的实根,求m的取值范围.
=m恰有两个不等的实根,求m的取值范围.
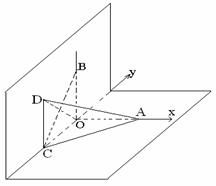
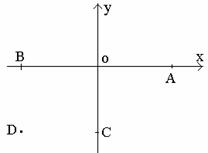
20.(本小题12分)在平面直角坐标系xoy中,已知四点A(2,0),B(-2,0),C(0,-2),D(-2,-2),把坐标系平面沿y轴折为直二面角.
(1)求证:BC⊥AD;
(2)求二面角C-AD-O的大小;
(3)求三棱锥C-AOD的体积.
19.(本小题12分)某部门为每位“志愿者”进行上岗培训,每人可以选择参加一项培训、参加两项培训或不参加培训,已知参加过礼仪培训的有75%,参加过实用语言培训的有60%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(1)任选1名“志愿者”,求该人参加过培训的概率;
(2)任选3名“志愿者”,记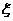 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求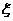 的分布列和期望.
的分布列和期望.
18.(本小题12分)已知向量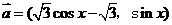 ,
,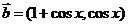 ,设
,设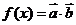 .
.
(1).求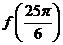 的值;
的值;
(2).当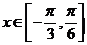 时,求函数
时,求函数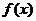 的值域。
的值域。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com