
18.在数列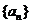 中,
中,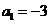 ,
,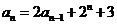
 .
.
(1)求 和
和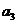 的值;
的值;
(2)设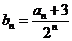
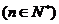 ,证明:
,证明: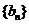 是等差数列.
是等差数列.
17.解:(1)取出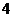 个球都是红球的概率为
个球都是红球的概率为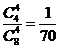 ,
,
取出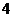 个球都是黑球的概率为
个球都是黑球的概率为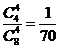 ,
,
所以取出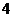 个球的颜色相同的概率为
个球的颜色相同的概率为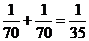 .
.
(2)由(1)可知,取出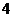 个球都是红球的概率为
个球都是红球的概率为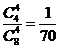 ,
,
取出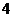 个球有
个球有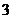 个红球
个红球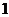 个黑球的概率为
个黑球的概率为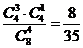 ,
,
取出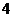 个球有
个球有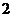 个红球
个红球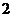 个黑球的概率为
个黑球的概率为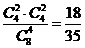 ,
,
所以获得奖品的概率为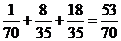 .
.
17.已知一口袋中有大小、质地均相同的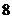 个球,其中有
个球,其中有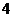 个红球和
个红球和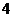 个黑球,
个黑球,
现从中任取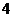 个球.
个球.
(1)求取出的球颜色相同的概率;
(2)若取出的红球数不少于黑球数,则可获得奖品,求获得奖品的概率.
16.解:(1)∵
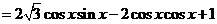
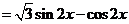
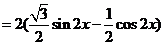
 ,
,
∴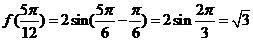 .
.
(2)∵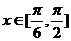 ,∴
,∴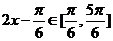 ,
,
∴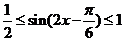 ,
,
∴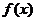 在区间
在区间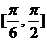 上的最小值为
上的最小值为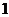 ,最大值为
,最大值为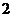 .
.
16.已知函数
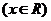 .
.
(1)求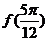 的值;
的值;
(2)求函数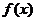 在区间
在区间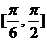 上的最小值和最大值.
上的最小值和最大值.
15.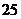
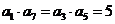 ,即
,即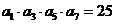 .
.
15.在等比数列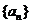 中,
中,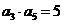 ,则
,则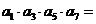 .
.
14.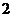 圆
圆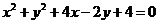 的标准方程为
的标准方程为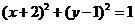 ,
,
即该圆的半径为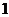 ,而点到直线
,而点到直线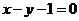 的最大距离与最小距离的
的最大距离与最小距离的
差为恰好为圆的直径,即距离的差为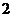 .
.
14.圆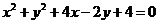 上的点到直线
上的点到直线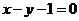 的最大距离与最小距离的
的最大距离与最小距离的
差为 .
13.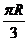 北纬
北纬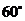 圈上的小圆的半径显然为
圈上的小圆的半径显然为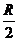 ,而
,而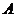 、
、 两地在此纬度圈上的
两地在此纬度圈上的
弧长为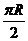 ,则
,则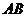 是小圆的直径,即
是小圆的直径,即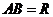 ,得
,得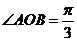 ,
,
所以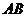 两地的球面距离为
两地的球面距离为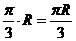 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com