
1.下列叙述中,正确的是( )
A.SARS病毒不具有细胞结构,所以不具有生命特征
B.一只草履虫就是一个细胞
C.精子不具有细胞结构,只有形成受精卵,才具有细胞的结构和功能
D.细胞是一切生物的结构单位和功能单位
22.证明:(1)∵平面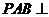 平面
平面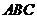 ,
,
平面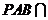 平面
平面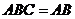 ,且
,且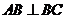 ,
,
∴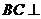 平面
平面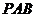 ,
,
又∵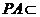 平面
平面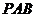 ,∴
,∴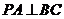 ,
,
又∵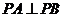 ,
,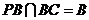 ,
,
 ∴
∴ 平面
平面 .
.
解:(2)作 于点
于点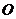 ,
,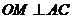 于点
于点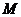 ,连结
,连结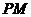 ,
,
∵平面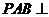 平面
平面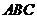 ,
,
∴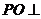 平面
平面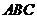 ,
,
由三垂线定理得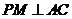 ,
,
∴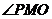 是二面角
是二面角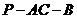 的平面角,
的平面角,
又∵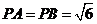 ,
,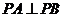 ,
,
∴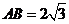 ,
,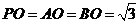 ,
,
在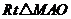 中,
中,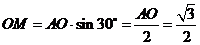 ,
,
∴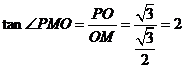 ,
,
∴二面角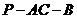 的平面角的正切值为
的平面角的正切值为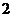 .
.
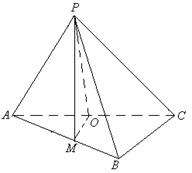
22.如图,在三棱锥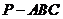 中,
中,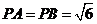 ,
,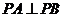 ,
,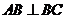 ,
,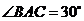 ,平面
,平面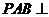 平面
平面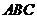 .
.
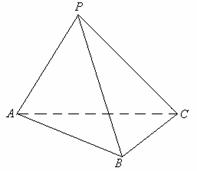 (1)求证:
(1)求证: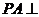 平面
平面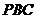 ;
;
(2)求二面角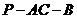 的平面角的正切值.
的平面角的正切值.
21.解:(1)∵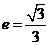 ,∴
,∴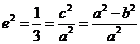 ,
,
∴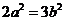 ,
,
又∵直线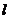 :
: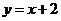 与圆
与圆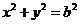 相切,
相切,
∴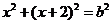 有两个相等的实数根
有两个相等的实数根 ,∴
,∴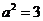 ,
,
∴椭圆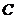 的方程为
的方程为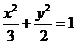 .
.
(2)由题意知,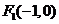 ,
,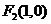 ,直线
,直线 :
: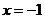 ,
,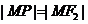 ,
,
所以动点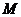 到定直线
到定直线 :
: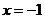 的距离等于它到定点
的距离等于它到定点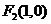 的距离,
的距离,
从而动点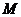 的轨迹是以
的轨迹是以 为准线,
为准线,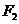 为焦点的抛物线
为焦点的抛物线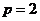 ,
,
因此,点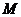 的轨迹方程为
的轨迹方程为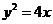 .
.
21.已知椭圆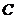 :
: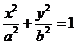
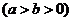 的离心率为
的离心率为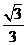 ,直线
,直线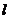 :
: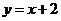 与
与
以原点为圆心、以椭圆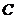 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆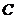 的方程;
的方程;
(2)设椭圆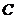 的左焦点为
的左焦点为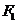 ,右焦点为
,右焦点为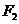 ,直线
,直线 过点
过点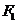 且垂直于椭圆的长轴,
且垂直于椭圆的长轴,
动直线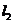 垂直
垂直 于点
于点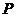 ,线段
,线段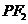 的垂直平分线交
的垂直平分线交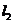 于点
于点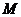 ,求点
,求点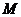 的轨迹方程.
的轨迹方程.
20.解:(1)∵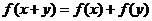 ,
,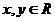
令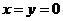 ,得
,得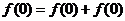
∴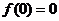 ,
,
再令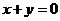 ,即
,即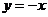 ,得
,得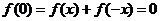 ,
,
∴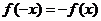 ,
,
∴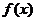 在
在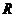 上是奇函数.
上是奇函数.
证明:(2)设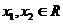 ,
, ,则
,则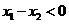 ,
,
∵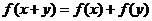 ,
,
∴ ,
,
又∵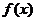 为奇函数,且当
为奇函数,且当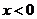 时,
时,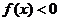 ,
,
∴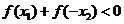 ,
,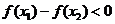 ,
,
∴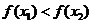 ,
,
∴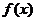 为
为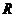 上的增函数.
上的增函数.
20.已知定义在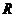 上的函数
上的函数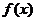 满足:
满足: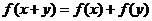 ,当
,当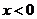 时,
时,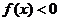 .
.
(1)求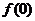 ,并证明
,并证明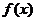 在
在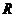 上是奇函数;
上是奇函数;
(2)求证: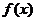 为
为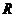 上的增函数.
上的增函数.
19.解:(1)∵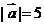 ,
,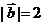 ,
, ,
,
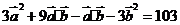 ,
,
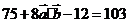 ,
,
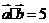 ,
,
∴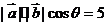 ,
,
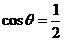 ,
,
∴求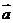 与
与 的夹角为
的夹角为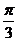 .
.
(2)在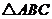 中,
中,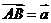 ,
,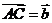 ,
,
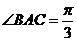 ,
,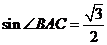 ,
,
∴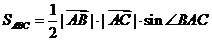
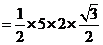
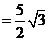 .
.
∴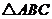 的面积为
的面积为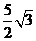 .
.
19.已知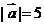 ,
,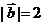 ,
, .
.
(1)求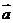 与
与 的夹角
的夹角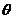 ;
;
(2)若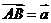 ,
,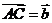 ,作
,作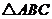 ,求
,求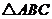 的面积.
的面积.
18.解:(1)∵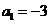 ,
,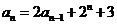
 ,
,
∴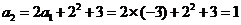 ,
,
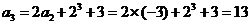 .
.
(2)对于任意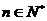 ,
,
∵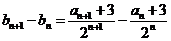
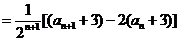
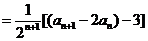
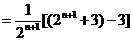
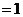 .
.
∴数列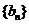 是首项为
是首项为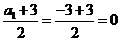 ,公差为
,公差为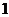 的等差数列.
的等差数列.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com