
22. (本题满分16分)已知函数f(x)=x3-ax-b (a,b∈R)
(1)当a=b=1时,求函数f(x)的单调区间
(2)是否存在a,b,使得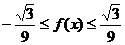 对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。
对任意的x∈[0,1]成立?若存在,求出a,b的值,若不存在,说明理由。
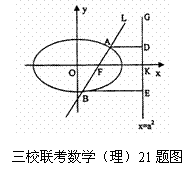
21. (本题满分14分)如图,已知直线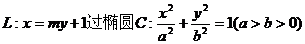 的右焦点F,且交椭圆C于A,B两点,点A,F,B在直线
的右焦点F,且交椭圆C于A,B两点,点A,F,B在直线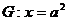 上的射影依次为点D,K,E.
上的射影依次为点D,K,E.
(1)若抛物线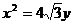 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)连接AE,BD,证明:当m变化时,直线AE、BD相交于一定点。
20.(本题满分14分)如图,在三棱拄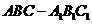 中,
中,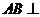 侧面
侧面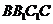 ,
,
已知AA1=2, ,
,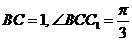
(Ⅰ)求证: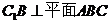 ;
;
(Ⅱ)试在棱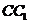 (不包含端点
(不包含端点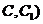 上确定一点
上确定一点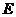 的位置,使得
的位置,使得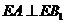 ;
;
(Ⅲ) 在(Ⅱ)的条件下,求二面角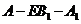 的平面角的正切值.
的平面角的正切值.
18. (本题满分14分)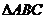 中,三个内角A、B、C所对的边分别为
中,三个内角A、B、C所对的边分别为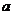 、
、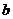 、
、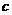 ,若
,若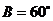 ,
,
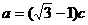 .
.
(1)求角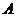 的大小;
的大小;
(2)已知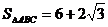 ,求函数
,求函数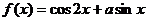 的最大值
的最大值
19. (本题满分14分)有一种舞台灯,外形是正六棱柱ABCDEF-A1B1C1D1E1F1,在其每一个侧面上(不在棱上)安装5只颜色各异的彩灯,假若每只灯正常发光的概率是0.5,若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面. 假定更换一个面需100元,用ξ表示维修一次的费用.
(1)求面ABB1A1需要维修的概率;
(2)写出ξ的分布列,并求ξ的数学期望.

17.在平面直角坐标系 ,已知平面区域 A={ (x,y)|
x + ty < 2,且t
,已知平面区域 A={ (x,y)|
x + ty < 2,且t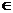 R,
R,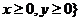 ,若平面区域B={ (x, y ) | (x+y, x-y )
,若平面区域B={ (x, y ) | (x+y, x-y )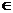 A }的面积不小于1,则t的取值范围为 ▲ .
A }的面积不小于1,则t的取值范围为 ▲ .
16.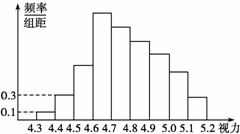 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图所示,由于不慎,部分数据丢失,但知道前四组的频数成等比数列,后六组的频数成等差数列,设最大频率为a,视 力在4.6到5.0之间的学生数为b,则a+b的值为 ▲
.
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图所示,由于不慎,部分数据丢失,但知道前四组的频数成等比数列,后六组的频数成等差数列,设最大频率为a,视 力在4.6到5.0之间的学生数为b,则a+b的值为 ▲
.
15.如图所示的流程图,若输出的结果是9,则判断框中的横线上可以填入的最大整数为 ▲ .
14.在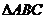 中,M是BC的中点,AM=3,点P在AM上且满足学
中,M是BC的中点,AM=3,点P在AM上且满足学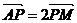 ,则
,则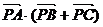 等于▲ .
等于▲ .
13.若关于x的方程x-+ k=0在x∈(0,1]没有实数根,则k的取值范围为 ▲ .
12.棱长为2的立方体的八个顶点都在球O的表面上,则球O的表面积是 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com