
5.解: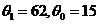 ,当
,当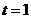 时,
时,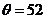 ,即
,即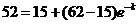 ,
,
得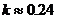 ,
,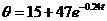 ,
,
当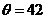 时,
时,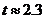 ,当
,当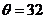 时,
时, ,
,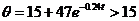 ,
,
即物体不会冷却到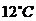 .
.
5.把物体放在冷空气中冷却,如果物体原来的温度是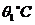 ,空气的温度是
,空气的温度是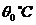 ,
,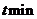 后物体的温度
后物体的温度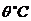 可由公式
可由公式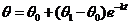 求得,这里
求得,这里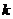 是一个随着物体与空气的接触状况而定的正的常数.现有
是一个随着物体与空气的接触状况而定的正的常数.现有 的物体,放在
的物体,放在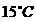 的空气中冷却,
的空气中冷却,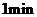 以后物体的温度是
以后物体的温度是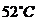 .求上式中
.求上式中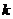 的值(精确到
的值(精确到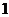 位有效数字),然后计算开始冷却后多长时间物体的温度是
位有效数字),然后计算开始冷却后多长时间物体的温度是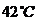 ,
,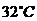 .物体会不会冷却到
.物体会不会冷却到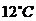 ?
?
4.证明:(1)∵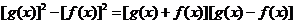
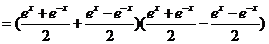
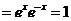 ,
,
∴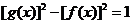 ;
;
(2)∵ ,
,
而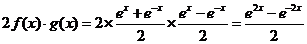 ,
,
∴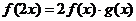 ;
;
(3)∵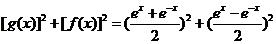
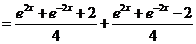
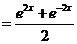 ,
,
而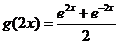 ,
,
∴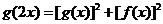 .
.
4.设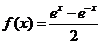 ,
,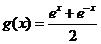 ,求证:(1)
,求证:(1)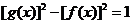 ;
;
(2)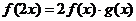 ;(3)
;(3)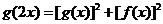 .
.
3.解:(1)设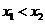 ,则
,则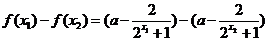
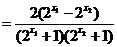 ,
,
由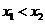 ,得
,得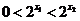 ,所以
,所以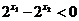 ,
,
得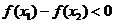 ,即
,即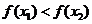 ,
,
所以不论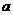 取任何实数,函数
取任何实数,函数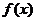 在
在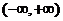 上是增函数.
上是增函数.
(2)函数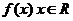 为奇函数,则
为奇函数,则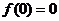 ,
,
即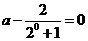 ,得
,得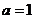 .
.
3.对于函数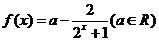 ;
;
(1)探索函数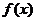 的单调性;
的单调性;
(2)是否存在实数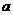 使函数
使函数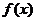 为奇函数?
为奇函数?
2.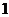
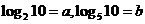 ,得
,得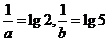 ,
,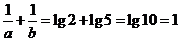 .
.
2.若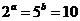 ,则
,则 ___________________.
___________________.
1.A 当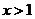 时,
时, ,即
,即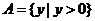 ,
,
当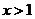 时,
时, ,即
,即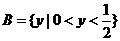 ,得
,得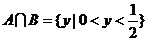 .
.
1.已知集合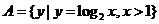 ,
,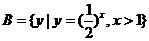 ,则
,则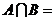 ( ).
( ).
A.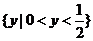 B.
B. 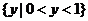 C.
C. 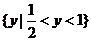 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com