
7. 解:(Ⅰ)因为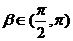 ,
,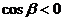 ………
……… …………………………………………………………2分
…………………………………………………………2分
又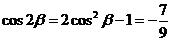 ,所以
,所以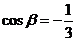 …………………………………………………6分(Ⅱ)根据(Ⅰ),得
…………………………………………………6分(Ⅱ)根据(Ⅰ),得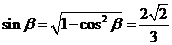 ………
……… ……………………………
…………………………… ……………… 8分而
……………… 8分而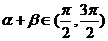 ,且
,且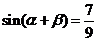 ,
,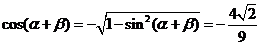 ……10分
……10分
故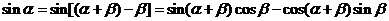 ……………………………12分
……………………………12分
=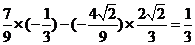 ………………………………………………………………………14分
………………………………………………………………………14分
6.解:⑴由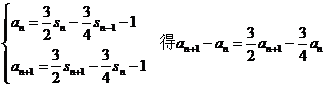
所以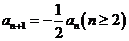
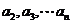 成等比……………3分
成等比……………3分
故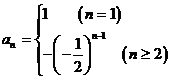 …………4分
…………4分
⑵依题意: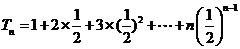
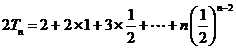
两式错们相减得: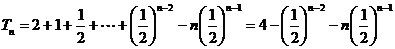
所以对一切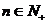 有
有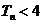 且
且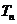 是递增的
是递增的
又因为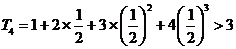
所以满足条件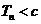 的最小正整数
的最小正整数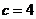 …………8分
…………8分
⑶记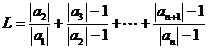
一方面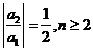 时
时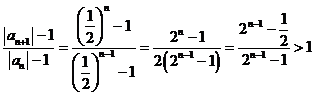
所以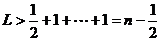 …………10分
…………10分
另一方面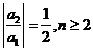 时
时
 (只有
(只有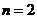 时取等)
时取等)
所以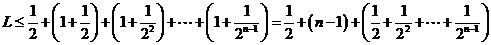
=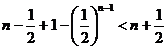 …………12分
…………12分
5.解⑴因为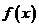 是二次函数,且
是二次函数,且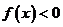 的解集是
的解集是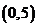
所以可设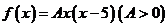
所以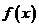 在区间
在区间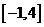 上最大值是
上最大值是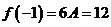 所以
所以 所以
所以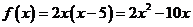 ………………6分
………………6分
⑵由已知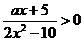 所以
所以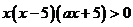 又
又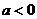
所以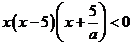 ……………
…………… …8分
…8分
①
若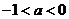 ,则
,则 所以
所以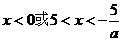
②
若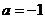 ,则
,则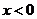
③
若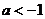 ,则
,则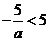 ,所以
,所以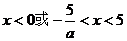 ………………11分
………………11分
综上知:当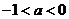 时,原不等式的解集为
时,原不等式的解集为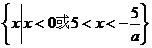
当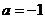 时,原不等式的解集为
时,原不等式的解集为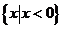
当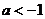 时,原不等式的解集为
时,原不等式的解集为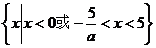 ……………12分
……………12分
4.因为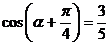
所以 ………2分
………2分
平方得: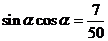 …………5分
…………5分
⑵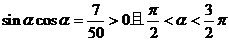 所以
所以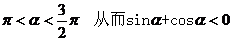
又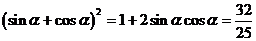
所以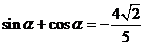 又
又
所以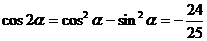 ……………………9分
……………………9分
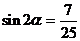 ………10分
………10分
故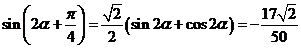 ……………12分
……………12分
3.解⑴设等差数列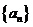 的公差是
的公差是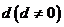 因为
因为
 成等比数列,所以
成等比数列,所以 ……………………………………2分
……………………………………2分
即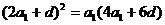 化简得
化简得 又a≠0所以
又a≠0所以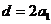 ……5分
……5分
所以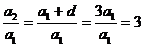 ……………………………………7分
……………………………………7分
 ⑵因为
⑵因为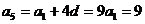
所以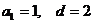 ………………
……………… ……………………9分
……………………9分
所以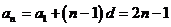 ……………………………………11分
……………………………………11分
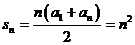 …………………………………13分
…………………………………13分
2.⑴因为
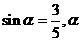 是第二象限角
是第二象限角
所以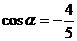 ……………………………………4分
……………………………………4分
从而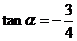 ……………………………………7分
……………………………………7分
⑵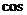
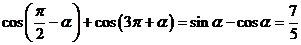 …………………………13分
…………………………13分
1.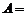
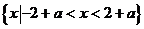 ……………………………………4分
……………………………………4分
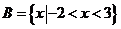 又
又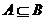 ……………………………………8分
……………………………………8分
所以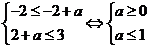 所以
所以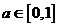 …………………………………13分
…………………………………13分
12. (本小题满分16分) 已知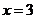 是函数
是函数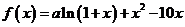 的一个极值点。
的一个极值点。
(Ⅰ)求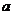 ;(Ⅱ)求函数
;(Ⅱ)求函数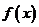 的单调区间;(Ⅲ)若直线
的单调区间;(Ⅲ)若直线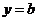 与函数
与函数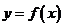 的图象有3个交点,
的图象有3个交点, 求
求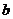 的取值范围。
的取值范围。
11. (本小题满分16分)已知数列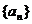 ,其前n项和Sn满足
,其前n项和Sn满足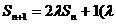 是大于0的
是大于0的
常数),且a1=1,a3=4.
(1)求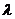 的值;
的值;
(2)求数列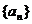 的通项公式an;
的通项公式an;
(3)设数列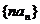 的前n项和为Tn,试比较
的前n项和为Tn,试比较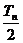 与Sn的大小.
与Sn的大小.
10. (本小题满分16分) 已知DABC的三个内角A,B,C对应的边长分别为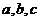 ,向量
,向量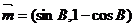 与向量
与向量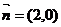 夹角
夹角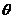 余弦值为
余弦值为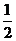 。
。
(1)求角B的大小;(2)DABC外接圆半径为1,求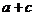 范围
范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com