
22.设数列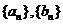 满足
满足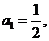
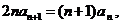 且
且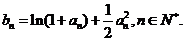
(1)求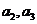 ,
,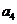 并求数列
并求数列 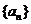 的通项公式;
的通项公式;
(2)对一切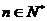 ,证明
,证明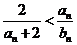 成立;
成立;
(3)记数列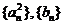 的前
的前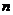 项和分别是
项和分别是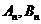 ,证明
,证明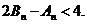
解:(1) 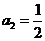 ,
, 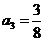 ,
,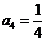 ……………………(2分)
……………………(2分)
由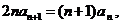 得
得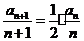 ……………………(3分)
……………………(3分)
即数列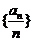 是以
是以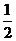 为首项,以
为首项,以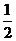 为公比的等比数列
为公比的等比数列
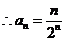 ……………………(4分)
……………………(4分)
注:用数学归纳法也可以。
(2)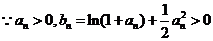
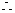 要证明
要证明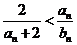 只需证明
只需证明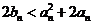
即证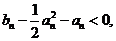 即证明
即证明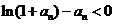 成立……………………(6分)
成立……………………(6分)
构造函数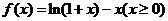 ……………………(7分)
……………………(7分)
则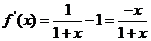 ,……………………(8分)
,……………………(8分)
当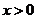 时,
时,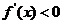 ,即
,即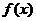 在
在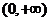 上单调递减,所以
上单调递减,所以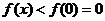
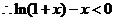 ,即
,即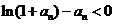 对一切
对一切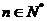 都成立,
都成立,
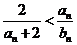 ……………………(10分)
……………………(10分)
(3)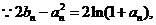
由(2)可知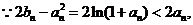
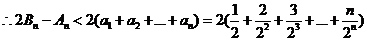 ……………………(12分)
……………………(12分)
利用错位相减法求得
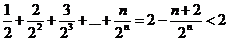
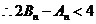 ……………………(14分)
……………………(14分)
21.如图所示,已知圆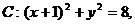 定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足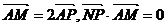 ,点N的轨迹为曲线E。
,点N的轨迹为曲线E。
(1)求曲线E的方程;
(2)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),且满足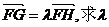 的取值范围。
的取值范围。

解:(1)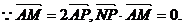
∴NP为AM的垂直平分线,
∴|NA|=|NM|……………………(1分)
又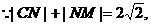
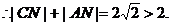 ……………………(2分)
……………………(2分)
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆……………………(3分)
且椭圆长轴长为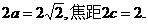
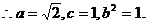 ……………………(5分)
……………………(5分)
∴曲线E的方程为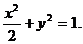 ……………………(6分)
……………………(6分)
(2)当直线GH斜率存在时,
设直线GH方程为
得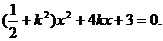 ……………………(7分)
……………………(7分)
由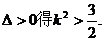 ……………………(8分)
……………………(8分)
设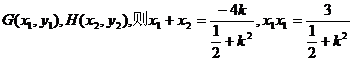 ……………………(9分)
……………………(9分)
又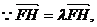
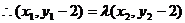
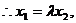
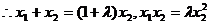
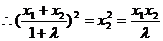
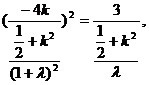
整理得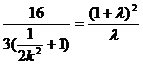 ……………………(10分)
……………………(10分)
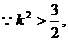
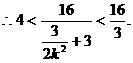
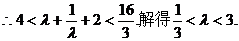 ……………………(11分)
……………………(11分)
又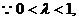
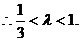 ……………………(12分)
……………………(12分)
又当直线GH斜率不存在,方程为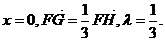
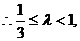 即所求
即所求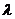 的取值范围是
的取值范围是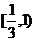 ……………………(14分)
……………………(14分)
20.已知函数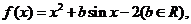
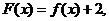 且对于任意实数
且对于任意实数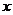 ,恒有
,恒有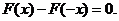
(1)求函数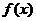 的解析式;
的解析式;
(2)已知函数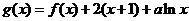 在区间
在区间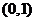 上单调递减,求实数
上单调递减,求实数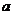 的取值范围;
的取值范围;
(3)函数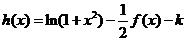 有几个零点?
有几个零点?
解:(1)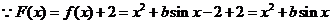 ,
,
依题意,对任意实数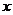 ,恒有
,恒有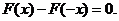
即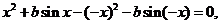
即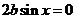
所以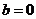 ,……………………(1分)
,……………………(1分)
所以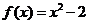 ……………………(2分)
……………………(2分)
(2)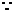
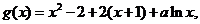
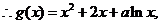
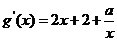 ……………………(3分)
……………………(3分)
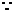 函数
函数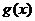 在(0,1)上单调递减,
在(0,1)上单调递减,
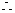 在区间(0,1)
在区间(0,1)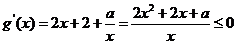 恒成立……………………(4分)
恒成立……………………(4分)
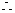
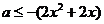 在(0,1)上恒成立
在(0,1)上恒成立
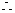 而
而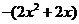 在(0,1)上单调递减
在(0,1)上单调递减
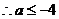 为所求。……………………(6分)
为所求。……………………(6分)
(3)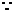
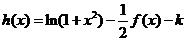 =
=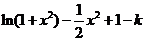
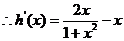
令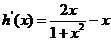 =0,解得
=0,解得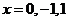
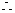 当
当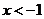 时,
时,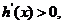 当
当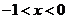 时,
时,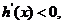
当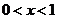 时,
时,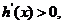 当
当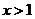 时,
时,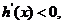
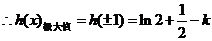 ……………………(7分)
……………………(7分)
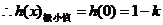 ……………………(8分)
……………………(8分)
所以①当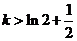 时,函数没有零点;……………………(9分)
时,函数没有零点;……………………(9分)
②当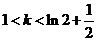 时,函数有四个零点;……………………(10分)
时,函数有四个零点;……………………(10分)
③当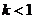 或
或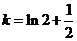 时,函数有两个零点;……………………(11分)
时,函数有两个零点;……………………(11分)
④当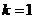 时,函数有三个零点;……………………(12分)
时,函数有三个零点;……………………(12分)
19.如图,在直三棱柱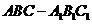 中,
中,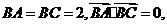 异面直线
异面直线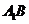 与
与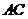 成
成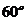 的角,点
的角,点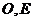 分别是棱
分别是棱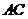 和
和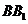 的中点,点
的中点,点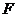 是棱
是棱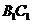 上的动点。
上的动点。

(1)证明: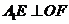 ;
;
(2)求点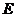 到平面
到平面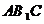 的距离;
的距离;
(3)求二面角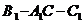 的大小。
的大小。
解:(1)取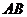 中点M,连接
中点M,连接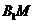 ,
,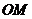
则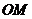
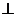 平面
平面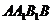 ,则
,则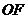 在平面
在平面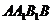 内的摄影为
内的摄影为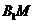 ,……………………(2分)
,……………………(2分)
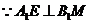
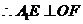 ……………………(4分)
……………………(4分)
(2)由体积转换可求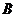 点到平面
点到平面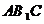 的距离为
的距离为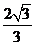 ,……………………(7分)
,……………………(7分)
而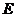 是
是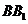 的中点
的中点
所以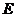 点到平面
点到平面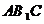 的距离为
的距离为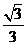 ……………………(8分)
……………………(8分)
(3)取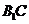 的中点
的中点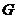 ,连接
,连接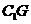 ,则
,则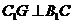 ,又
,又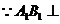 平面
平面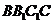
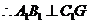
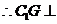 平面
平面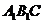 ,作
,作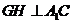 于
于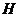 ,连接
,连接
所以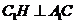
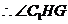 是所求二面角的平面角……………………(10分)
是所求二面角的平面角……………………(10分)
易得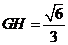 ,又
,又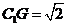
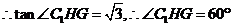
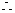 所求二面角的平面角为
所求二面角的平面角为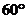 ……………………(12分)
……………………(12分)
另解:空间向量方法
(1)同上……………………(4分)
(2)如图,以 点为坐标原点,分别以
点为坐标原点,分别以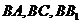 所在直线为
所在直线为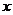 轴,
轴,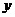 轴,
轴,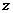 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则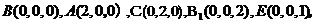
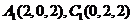
……………………(5分)
设平面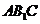 的法向量为
的法向量为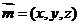
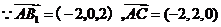
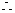 求得平面
求得平面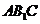 的法向量为
的法向量为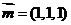 ……………………(6分)
……………………(6分)
又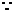
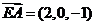
所以,点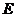 到平面
到平面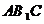 的距离
的距离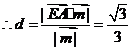 ……………………(8分)
……………………(8分)
(3)设平面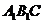 的法向量为
的法向量为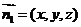
可求得平面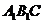 的法向量为
的法向量为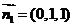 ……………………(9分)
……………………(9分)
同理可求得平面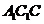 的法向量为
的法向量为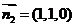 ……………………(10分)
……………………(10分)
所以,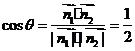 ……………………(11分)
……………………(11分)
所以二面角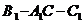 的大小为
的大小为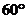 ……………………(12分)
……………………(12分)
18.为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡)。某旅游公司
组织了一个有36名游客的旅游团到四川名胜旅游,其中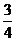 是省外游客,其余是省内游客。 在省外游客中有
是省外游客,其余是省内游客。 在省外游客中有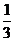 持金卡,在省内游客中有
持金卡,在省内游客中有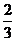 持银卡。
持银卡。
(I)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(II)在该团的省内游客中随机采访3名游客,设其中持银卡人数为随机变量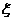 ,求
,求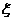 的分布列及数学期望
的分布列及数学期望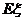 。
。
解:(Ⅰ)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡。设事件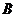 为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”, 事件
为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”, 事件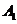 为“采访该团3人中,1人持金卡,0人持银卡”, 事件
为“采访该团3人中,1人持金卡,0人持银卡”, 事件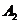 为“采访该团3人中,1人持金卡,1人持银卡”。
为“采访该团3人中,1人持金卡,1人持银卡”。
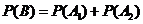 ……………………(2分)
……………………(2分)
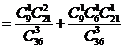
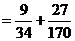 ……………………(4分)
……………………(4分)
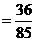
所以在该团中随机采访3人,恰有1人持金卡且持银卡者少于2人的概率是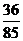 。
。
…………………………………………………………6分
(Ⅱ)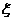 的可能取值为0,1,2,3
的可能取值为0,1,2,3
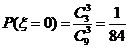 , ……………………(7分)
, ……………………(7分)
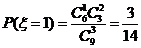 ……………………(8分)
……………………(8分)
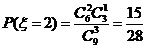 ,……………………(9分)
,……………………(9分)
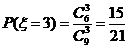 , ……………………(10分)
, ……………………(10分)
所以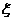 的分布列为
的分布列为
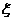 |
0 |
1 |
2 |
3 |
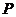 |
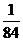 |
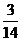 |
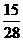 |
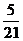 |
所以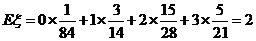 , ……………………12分
, ……………………12分
17.设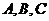 为
为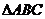 的三个内角,
的三个内角,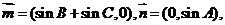 且
且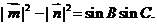
(1)求角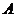 的大小;
的大小;
(2)求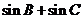 的取值范围。
的取值范围。
解:(1)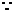
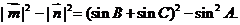
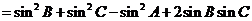
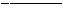 (2分)
(2分)
依题意有,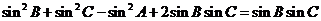
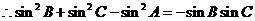
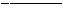 (3分)
(3分)
由正弦定理,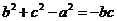 ……………..(4分)
……………..(4分)
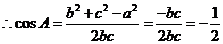 ……….(5分)
……….(5分)
所以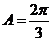 ………(6分)
………(6分)
(2)
=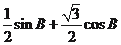 ………(8分)
………(8分)
=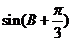 ………(9分)
………(9分)
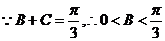
则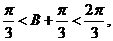 ………(10分)
………(10分)
则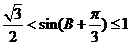 ,即
,即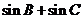
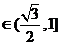 ……(12分)
……(12分)
16.在棱长为2的正方体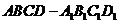 中,正方形
中,正方形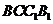 所在平面内的动点
所在平面内的动点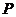 到直线
到直线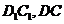 的距离之和为
的距离之和为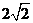 ,则
,则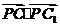 有最大值
有最大值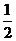 .
.
15.在极坐标系中,直线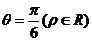 截圆
截圆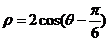 所得的弦长是 2 .
所得的弦长是 2 .
14.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 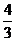
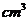 .
.
13.某程序框图如图所示,该程序运行后输出的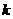 的值是 4 .
的值是 4 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com