
12.[解析](1)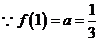 ,
,
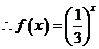
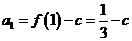 ,
,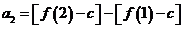
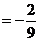 ,
,
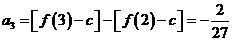 .又数列
.又数列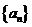 成等比数列,
成等比数列,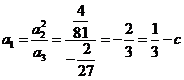 ,所以
,所以 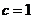 ;
;
又公比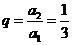 ,所以
,所以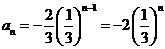
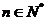 ;
;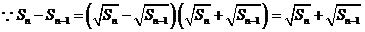
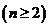
又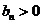 ,
,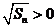 ,
, 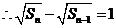 ;
;
数列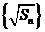 构成一个首相为1公差为1的等差数列,
构成一个首相为1公差为1的等差数列,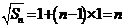 ,
, 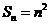
当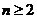 ,
, 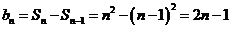 ;
;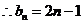 (
(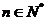 );
);
(2)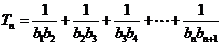
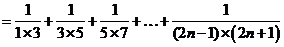
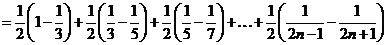

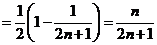 ;
;
由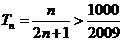 得
得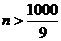 ,满足
,满足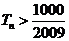 的最小正整数为112.
的最小正整数为112.
11.解: (1)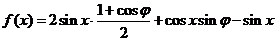
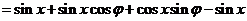
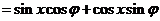
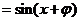
因为函数f(x)在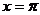 处取最小值,所以
处取最小值,所以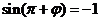 ,由诱导公式知
,由诱导公式知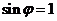 ,因为
,因为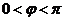 ,所以
,所以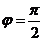 .所以
.所以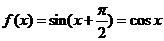
(2)因为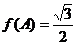 ,所以
,所以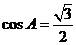 ,因为角A为
,因为角A为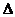 ABC的内角,所以
ABC的内角,所以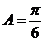 .又因为
.又因为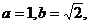 所以由正弦定理,得
所以由正弦定理,得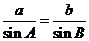 ,也就是
,也就是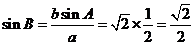 ,
,
因为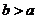 ,所以
,所以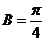 或
或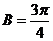 .当
.当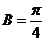 时,
时,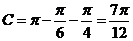 ;当
;当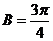 时,
时,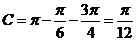 .
.
6.解:(1)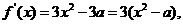
当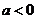 时,对
时,对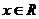 ,有
,有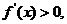
所以当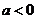 时,
时,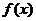 的单调增区间为
的单调增区间为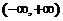
当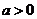 时,由
时,由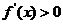 解得
解得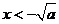 或
或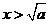 ;
;
由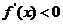 解得
解得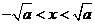 ,
,
当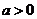 时,
时,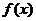 的单调增区间为
的单调增区间为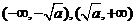 ;
;
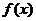 的单调减区间为
的单调减区间为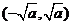 .……………………6分
.……………………6分
(2)因为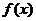 在
在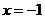 处取得极大值,
处取得极大值,
所以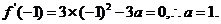
所以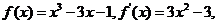
由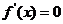 解得
解得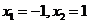 。
。
由(1)中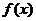 的单调性可知,
的单调性可知,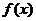 在
在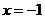 处取得极大值
处取得极大值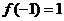 ,
,
在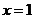 处取得极小值
处取得极小值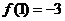 。
。
因为直线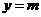 与
与 函数
函数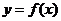 的图象有三个不同的交点,又
的图象有三个不同的交点,又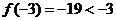 ,
,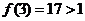 ,
,
结合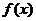 的单调性可知,
的单调性可知,
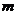 的取值范围是
的取值范围是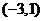 .……………………12分
.……………………12分
7[证法一]由已知,f(x)=|lgx|=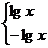
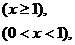 图象如下图。
图象如下图。
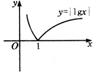
∵0<a<b,f(a)>f(b),∴a、b不可能同时在区间[1,+∞)上。
又由于0<a<b,故必有a∈(0,1).
①若b∈(0,1),显然有ab<1;②若b∈[1,+∞),由f(a)>f(b)有-lga>lgb.∴lg(ab)<0,ab<1.
综上,ab<1成立。
[证法二]∵f(a)>f(b),∴|lga|>|lgb|.从而(lga)2>(lgb)2,(lga+lgb)(lga-lgb)>0,
lg(ab)·lg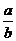 >0.
>0.
∵0<a<b,
∴0<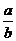 <1,lg
<1,lg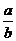 <0. ∴lg(ab)<0,ab<1.
<0. ∴lg(ab)<0,ab<1.
8解法一:在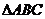 中
中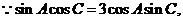 则由正弦定理及余弦定理有:
则由正弦定理及余弦定理有: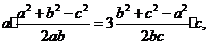 化简并整理得:
化简并整理得: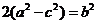 .又由已知
.又由已知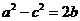
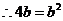 .解得
.解得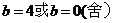 .
.
解法二:由余弦定理得: 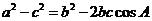 .又
.又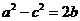 ,
,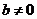 。
。
所以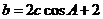 …………………………………①
…………………………………①
又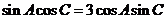 ,
,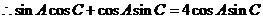
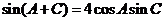 ,即
,即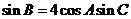
由正弦定理得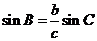 ,故
,故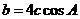 ………………………②
………………………②
由①,②解得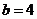 。
。
9
10解:解:∵函数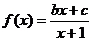 的图象过原点,
的图象过原点,
∴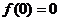 即
即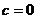 , ∴
, ∴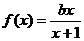 .
.
又函数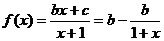 的图象关于点
的图象关于点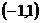 成中心对称,
成中心对称,
∴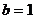 ,
,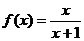 .
.
(2)解:由题意有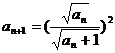 即
即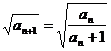 ,
,
即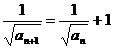 ,即
,即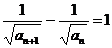 .
.
∴数列{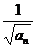 }是以1为首项,1为公差的等差数列.
}是以1为首项,1为公差的等差数列.
∴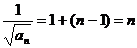 ,即
,即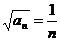 . ∴
. ∴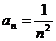 .
.
∴ 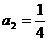 ,
,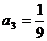 ,
,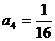 ,
,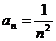 .
.
5、解:(1)证明:∵CB⊥侧面PAB,PF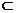 平面PAB,∴PF⊥BC,
平面PAB,∴PF⊥BC,
又∵△PAB是等边三角形,F是线段AB的中点,∴PF⊥AB,
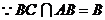 ∴PF⊥
∴PF⊥ 平面ABCD,
平面ABCD,
而D F
F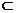 平面ABCD,∴DF⊥PF。……………………5分
平面ABCD,∴DF⊥PF。……………………5分
(2)方法一:
作CH⊥DF,垂足为H,连接PH,
由(1)知:PF⊥ 平面ABCD。
平面ABCD。
∴平面PDF⊥平面C DF,
DF,
∴CH⊥平面PDF,
∴PH是PC在平面PDF上的射影,
∴∠CPH是PC与平面PDF所成的角。
∵CB⊥侧面PAB,AD//BC,DA⊥侧面PAB,
∴△DAF,△BFC,△PBC都是直角三角形,
BC=1,则DA=AB=2,AF=FB=1,
在三角形DFC中,DF=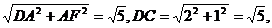
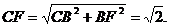 可求得
可求得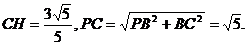
∴直角三角形PHC中,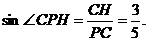
∴PC与平面PDF所成的角为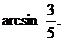 ……………………12分
……………………12分
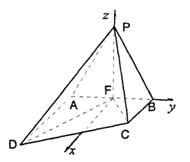 方法二:
方法二:
如图,以F为原点,建立空间直角坐标系。
BC=1,则DA=AB=2,AF=FB=1,PF=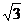
从而C(1,1,0 )、D(2,-1,0)、P(0,0
)、D(2,-1,0)、P(0,0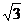 )
)
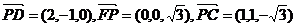
设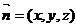 为平面PDF的法向量,由
为平面PDF的法向量,由
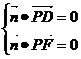
 ,可求得
,可求得
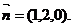
设PC与平面PDF所成的角为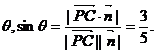
∴PC与平面PDF所成的角为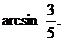 ……………………12分
……………………12分
4、解:展开式的通项为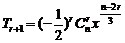 ,r=0,1,2,…,n
,r=0,1,2,…,n
由已知: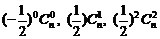 成等差数列
成等差数列
∴ 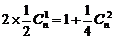 ∴ n=8 ……………………4分
∴ n=8 ……………………4分
(1)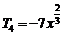 ……………………6分
……………………6分
(2)令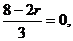 得
得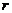 =4,常数项为
=4,常数项为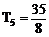 …………………………9分
…………………………9分
(3)令x=1,各项系数和为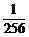 ……12分
……12分
3、解:⑴设甲、乙两人考试合格的事件分别为A、B,则
P(A)=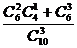 =
=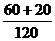 =
=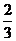 , P(B)=
, P(B)=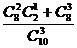 =
=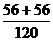 =
=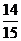 .
.
答:甲、乙两人考试合格的概率分别为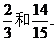 ……………………6分
……………………6分
⑵解法一、因为事件A、B相互独立,所以甲、乙两人考试均不合格的概率为
P(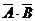 )=P(
)=P(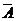 )P(
)P(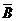 )=(1-
)=(1-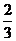 )(1-
)(1-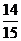 )=
)=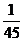 .
.
∴甲、乙两人至少有一人考试合格的概率为
P=1-P(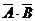 )=1-
)=1-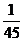 =
=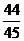 .
.
答:甲、乙两人至少有一人考试合格的概率为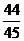 .……………………12分
.……………………12分
解法二:因为事件A、B相互独立,所以甲、乙两人至少有一人考试合格的概率为
 P=P(A·
P=P(A·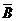 )+P(
)+P(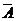 ·B)+P(A·B)=P(A)P(
·B)+P(A·B)=P(A)P(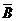 )+P(
)+P(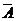 )P(B)+P(A)P(B)
)P(B)+P(A)P(B)
=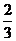 ×
×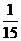 +
+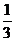 ×
×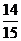 +
+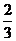 ×
×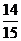 =
=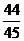 .
.
答:甲、乙两人至少有一人考试合格的概率为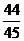 .……………………12分
.……………………12分
2、解:由题意可知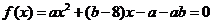 的两根分别为
的两根分别为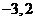 ,且
,且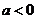 ,
,
则由韦达定理可得: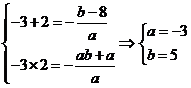 .
.
故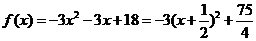 ……………………4分
……………………4分
(1)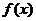 在
在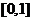 内单调递减,故
内单调递减,故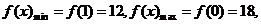
故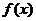 在
在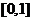 内的值域为
内的值域为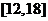 . ……………………8分
. ……………………8分
(2)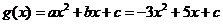 ,则要使
,则要使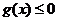 的解集为R,只需要方程
的解集为R,只需要方程
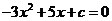 的判别式
的判别式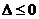 ,即
,即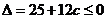 ,解得
,解得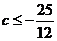 .
.
∴当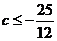 时,
时,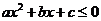 的解集为
的解集为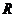 . ……………………12分
. ……………………12分
1、解:(1)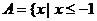 或
或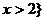 [来源:]
[来源:]
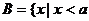 或
或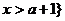 ……………………4分
……………………4分
(2)由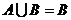 得
得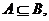 因此
因此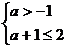
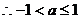
∴实数a的取值范围是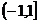 ……………………10分
……………………10分
12.(本小题满分12分,每小题6分)
已知点(1,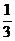 )是函数
)是函数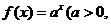 且
且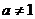 )的图象上一点,等比数列
)的图象上一点,等比数列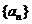 的前
的前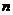 项和为
项和为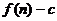 ,数列
,数列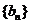
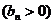 的首项为
的首项为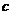 ,且前
,且前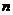 项和
项和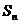 满足
满足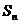 -
-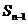 =
=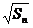 +
+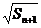 (
(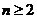 ).
).
(1)求数列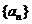 和
和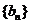 的通项公式;
的通项公式;
(2)若数列{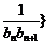 前
前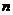 项和
项和 为
为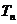 ,问
,问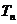 >
>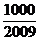 的最小正整数
的最小正整数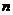 是多少?
是多少?
11.(本小题满分12分,每小题6分)
设函数f(x)=2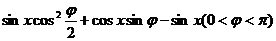 在
在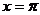 处取最小值.
处取最小值.
(1) 求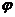 .的值;
.的值;
(2) 在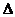 ABC中,
ABC中,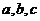 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知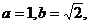
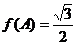 ,求角C.. www.5utk.co
,求角C.. www.5utk.co
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com