
(1) “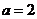 ”是“直线
”是“直线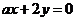 平行于直线
平行于直线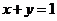 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(2) 若复数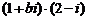 是纯虚数(
是纯虚数(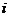 是虚数单位,
是虚数单位,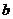 是实数),则
是实数),则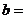
(A)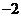 (B)
(B)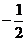 (C)
(C)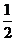 (D)2
(D)2
(3) 设全集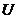 是实数集
是实数集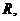
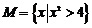 ,
,
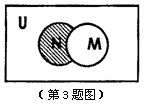
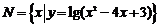 ,则图中阴影部分所表示的集合是
,则图中阴影部分所表示的集合是
(A)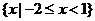 (B)
(B)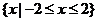
(C)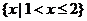 (D)
(D)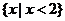
(4)在 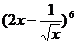 的展开式中的常数项为
的展开式中的常数项为
(A)15 (B)-15 (C)60 (D)- 60
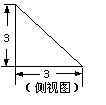
 (5) 一个几何体的三视图及其尺寸如图(单位:cm),
(5) 一个几何体的三视图及其尺寸如图(单位:cm),
则该几何体的体积是
|
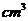 (B)
(B)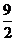
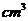
|
 (C)9
(C)9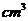 (D)
(D)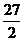
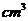
|
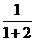 ,
,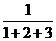 ,
,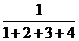 ,
,
…,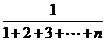 ,…的前
,…的前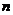 项和为
项和为
(A)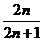 (B)
(B)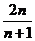 (C)
(C)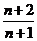 (D)
(D)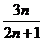
 (7)若直线
(7)若直线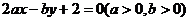 被圆
被圆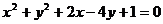 截得的弦长为4,则
截得的弦长为4,则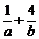 的最小值是
的最小值是
(A)5 (B)6
(C)8 (D)9
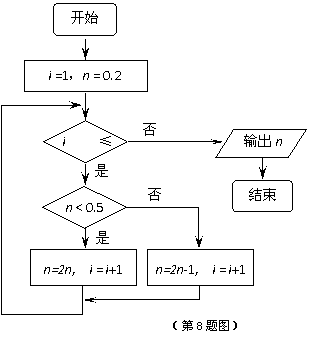
(8)右图所示的算法框图执行后输出的结果是
(A)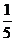 (B)
(B)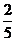
(C)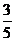 (D)
(D)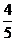
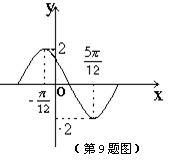 (9)已知函数
(9)已知函数 的导函数
的导函数 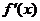 在一个周期内的图象如图所示, 则函数
在一个周期内的图象如图所示, 则函数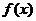 的解析式可以是
的解析式可以是
(A)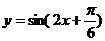 (B)
(B)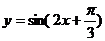
(C)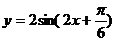 (D)
(D)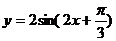
(10)已知各棱长均为1的四面体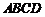 中,
中,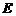 是
是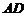 的中点,
的中点,
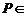 直线
直线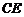 ,则
,则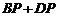 的最小值为
的最小值为
(A)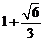 (B)
(B)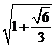 (C)
(C)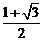 (D)
(D)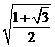
|
18. |
请在各题目的答题区域内作答,超出边框限定区域的答案无效
 19. 19.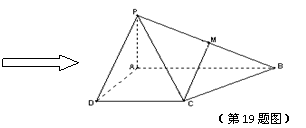 |
|
20. |
请在各题目的答题区域内作答,超出边框限定区域的答案无效
|
21. |
请在各题目的答题区域内作答,超出边框限定区域的答案无效
|
22. |
 请在各题目的答题区域内作答,超出边框限定区域的答案无效
请在各题目的答题区域内作答,超出边框限定区域的答案无效
台州市2010年高三年级第一次调考试题
17.
15. 16.
13. 14.________________________
11.________________________ 12.________________________
(18)(本题满分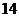 分)已知向量
分)已知向量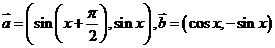 ,
,
函数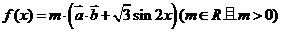 .
.
(Ⅰ)求函数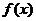 的最小正周期;
的最小正周期;
(Ⅱ)将函数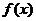 的图象的纵坐标保持不变,横坐标扩大到原来的两倍,然后再向右平移
的图象的纵坐标保持不变,横坐标扩大到原来的两倍,然后再向右平移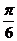 个单位得到
个单位得到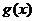 的图象,试探讨:当
的图象,试探讨:当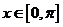 时,函数
时,函数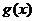 与
与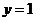 的图象的交点个数.
的图象的交点个数.
(19)(本题满分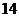 分)
分)
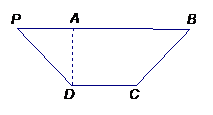
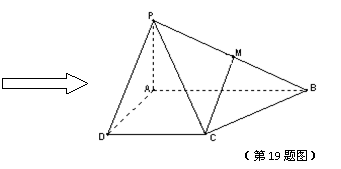
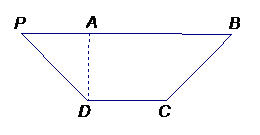
如图,在等腰梯形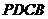 中,
中,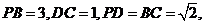
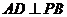 ,将
,将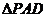 沿
沿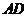 折起,使平面
折起,使平面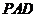 ⊥平面
⊥平面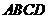 .
.
(Ⅰ)求证: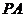 ⊥平面
⊥平面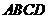 ;
;
(Ⅱ)求二面角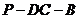 的大小;
的大小;
(Ⅲ)若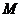 是侧棱
是侧棱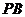 中点,求直线
中点,求直线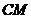 与平面
与平面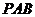 所成角的正弦值.
所成角的正弦值.
(20)(本题满分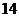 分)
分)
数列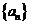 中,
中,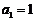 ,当
,当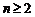 时,其前
时,其前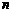 项的和
项的和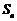 满足
满足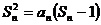 .
.
(Ⅰ)证明:数列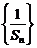 是等差数列;
是等差数列;
(Ⅱ)设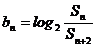 ,数列
,数列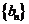 的前
的前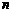 项和为
项和为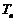 ,求满足
,求满足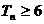 的最小正整数
的最小正整数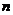 .
.
(21)(本题满分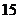 分)
分)
已知函数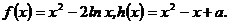
(Ⅰ)求函数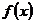 的极值;
的极值;
(Ⅱ)设函数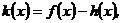 若函数
若函数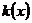 在
在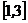 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数
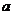 的取值范围.
的取值范围.
(22)(本题满分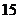 分)已知曲线
分)已知曲线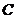 上的动点
上的动点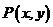 满足到点
满足到点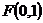 的距离比到直线
的距离比到直线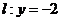 的距离小
的距离小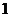 .
.
(Ⅰ)求曲线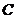 的方程;
的方程;
(Ⅱ)动点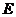 在直线
在直线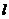 上,过点
上,过点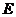 分别作曲线
分别作曲线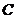 的切线
的切线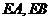 ,切点为
,切点为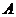 、
、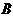 .
.
(ⅰ)求证:直线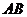 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;
(ⅱ)在直线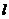 上是否存在一点
上是否存在一点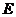 ,使得
,使得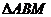 为等边三角形(
为等边三角形(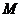 点也在直线
点也在直线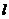 上)?若存在,求出点
上)?若存在,求出点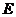 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.

 台州市2010年高三年级第一次调考试题
台州市2010年高三年级第一次调考试题
数 学(文) 答 题 卷 2010.3
(11)某赛季,甲乙两名篮球运动员都参加了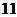 场比赛,他们每场
场比赛,他们每场
比赛得分的情况用右图所示的茎叶图表示,若
甲运动员的中位数为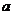 , 乙运动员的众数为
, 乙运动员的众数为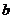 ,则
,则
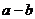 = ▲ .
= ▲ .
(12)在等比数列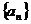 (
(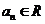 )
)
|
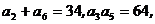
则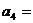 ▲ .
▲ .
(13)我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求
动点轨迹方程的方法,可以求出过点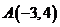 ,且法向量为
,且法向量为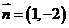 的直线(点法式)
的直线(点法式)
方程为: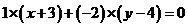 ,化简得
,化简得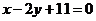 .类比以上方法,在空
.类比以上方法,在空
间直角坐标系中,经过点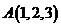 且法向量为
且法向量为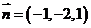 的平面(点法式)方程为:
的平面(点法式)方程为:
▲ .(请写出化简后的结果.)
(14)若直线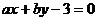 切圆
切圆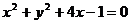 于点
于点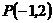 ,则
,则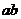 的值为 ▲ .
的值为 ▲ .
(15)甲盒子中装有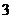 个编号分别为
个编号分别为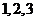 的小球,乙盒子中装有
的小球,乙盒子中装有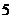 个编号分别为
个编号分别为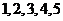 的小球,从甲、乙两个盒子中各随机取一个小球,则取出两小球编号之积为奇数的概率为
的小球,从甲、乙两个盒子中各随机取一个小球,则取出两小球编号之积为奇数的概率为
▲ .
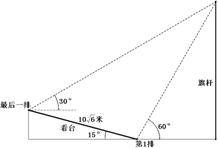 (16)某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度
(16)某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度
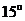 的看台的某一列的正前方,从这一列的第一排和最
的看台的某一列的正前方,从这一列的第一排和最
后一排测得旗杆顶部的仰角分别为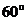 和
和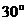 ,第一排
,第一排
和最后一排的距离为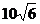 米(如图所示),旗杆底部
米(如图所示),旗杆底部
与第一排在一个水平面上.若国歌长度约为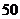 秒,升旗
秒,升旗
手应以 ▲ (米 /
|
(17)已知函数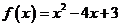 ,若实数
,若实数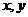 满足条件
满足条件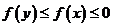 ,则
,则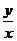 的取值范围为
▲ .
的取值范围为
▲ .
22.(本小题满分14分)
分别以双曲线G: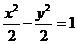 的焦点为顶点,以双曲线G的顶点为焦点作椭圆C,过椭圆C的右焦点作与x、y两轴均不垂直的直线l交椭圆于A、B两点.
的焦点为顶点,以双曲线G的顶点为焦点作椭圆C,过椭圆C的右焦点作与x、y两轴均不垂直的直线l交椭圆于A、B两点.
(Ⅰ)求椭圆C的方程;
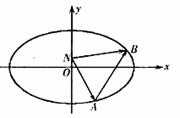 (Ⅱ)在y轴上是否存在点
(Ⅱ)在y轴上是否存在点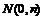 ,使得
,使得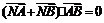 ?若存在,求出n的取值范围;若不存在,说明理由.
?若存在,求出n的取值范围;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com