
22、(18分) 对于定义在D上的函数 ,若存在
,若存在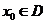 ,对任意的
,对任意的 ,都有
,都有 ,则称函数
,则称函数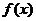 在区间
在区间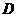 上有下界,把
上有下界,把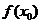 称为函数
称为函数 的“下界”。
的“下界”。
(1)分别判断下列函数是否有“下界”?如果有,写出“下界”否则请说明理由;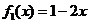
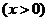 ,
,
(2)请你类比函数有“下界”的定义,写出函数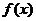 在区间
在区间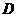 上有“上界”的定义;
上有“上界”的定义;
并判断函数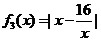 (
(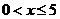 )是否有“上界”?说明理由;
)是否有“上界”?说明理由;
(3)若函数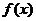 在区间
在区间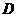 上既有“上界”又有“下界”,则称函数
上既有“上界”又有“下界”,则称函数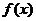 是区间
是区间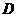 上的“有界函数”,把“上界”减去
“下界”的差称为函数
上的“有界函数”,把“上界”减去
“下界”的差称为函数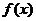 在
在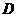 上的“幅度
上的“幅度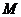 ”。
”。
对于实数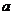 ,试探究函数
,试探究函数 是否是
是否是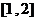 上的“有界函数”?如果是,求出“幅度
上的“有界函数”?如果是,求出“幅度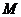 ”的值。
”的值。
解:
21、(16分)在直角坐标系 中,动点
中,动点 到两点
到两点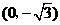 ,
,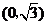 的距离之和
的距离之和
等于4,设动点 的轨迹为
的轨迹为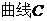 ,直线
,直线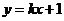 与
与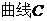 交于
交于 两点.
两点.
(1)写出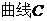 的方程;
的方程;
(2)若以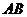 为直径的圆过坐标原点,求k的值
为直径的圆过坐标原点,求k的值
(3)求三角形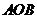 面积的最大值
面积的最大值
解:
20、 (14分)如图直三棱柱
(14分)如图直三棱柱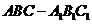 的侧棱长为2,底面
的侧棱长为2,底面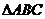 是等腰直角三角形,
是等腰直角三角形,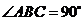 ,
,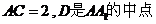
求(1)异面直线 所成的角的大小
所成的角的大小
(2)直线 与平面
与平面 所成的角
所成的角
解:
19、(12分)已知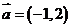 是过
是过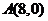 ,
, 两点的直线的方向向量,其中
两点的直线的方向向量,其中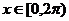 。
。
(1)当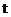 =15时,求
=15时,求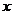 的值
的值
(2)求函数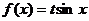 的最大值和最小值.
的最大值和最小值.
解:
18、已知圆M: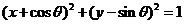 ,直线
,直线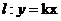 ,下面四个命题
,下面四个命题
①对任意实数k和 ,直线
,直线 和圆M相切;
和圆M相切;
②对任意实数k和 ,直线
,直线 和圆M有公共点;
和圆M有公共点;
③对任意实数 ,必存在实数
,必存在实数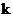 ,使得直线
,使得直线 和圆M相切;
和圆M相切;
④对任意给定的实数k,必存在实数 ,使得直线
,使得直线 和圆M相切
和圆M相切
其中真命题是 ( )
A.①② B.②③ C.②④ D.①③④
17、设函数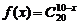 ,集合
,集合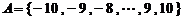 ,
,
判断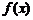 在
在 上的奇偶性为( )
上的奇偶性为( )
A. 偶函数 B .奇函数 C. 非奇非偶函数 D. 既是奇函数又是偶函数
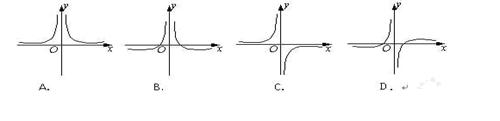
16、函数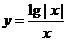 的图象大致是 ( )
的图象大致是 ( )
15、已知集合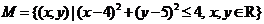 ,
,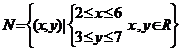
则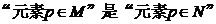 的 ------------( )条件
的 ------------( )条件
A. 充分非必要 B. 必要非充分 C. 充分必要 D.非充分非必要
14、右表给出一个“直角三角形数阵”:每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第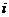 行第
行第 列的数为
列的数为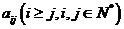 ,则
,则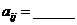
13、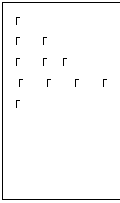 已知
已知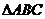 的三个顶点在以
的三个顶点在以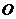 为球心的球面上,且
为球心的球面上,且
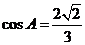 ,
,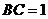 ,
,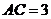 .若球的表面积为
.若球的表面积为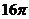 ,则
,则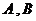
两点的球面距离是____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com