
21.(本小题满分14分)证明:(1)设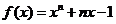 ,
,
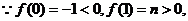 且函数
且函数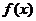 的图象在
的图象在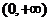 上是连续的,
上是连续的,
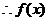 在
在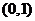 上至少有一个零点,即方程
上至少有一个零点,即方程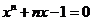 在
在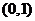 内至少有一个根.……… 3分
内至少有一个根.……… 3分
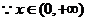 ,
,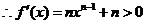 ,
,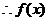 在
在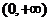 上是增函数.
上是增函数.
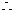 方程
方程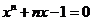 在
在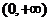 内有唯一根,且根在
内有唯一根,且根在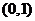 内,即
内,即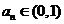 .………… 5分
.………… 5分
(2)方法一: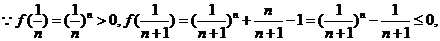
且函数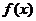 的图象在
的图象在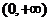 上是连续的,
上是连续的,
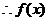 在
在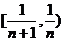 内至少有一个零点,即方程
内至少有一个零点,即方程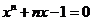 在
在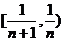 内至少有一个根.
内至少有一个根.
又由(1)知函数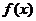 在
在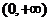 上单调递增,
上单调递增,
 方程
方程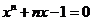 在
在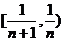 内有唯一根,
内有唯一根,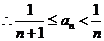 .……………………… 8分
.……………………… 8分
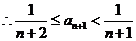 ,
,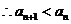 . …………………………………… 9分
. …………………………………… 9分
方法二:由(1)知,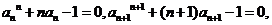 两式相减得:
两式相减得:
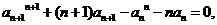 …………………………………7分
…………………………………7分
若存在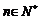 ,使得
,使得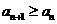 ,则
,则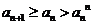 ,从而
,从而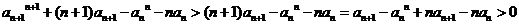 ,矛盾.
,矛盾.
所以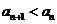 .
……………………………………… 9分
.
……………………………………… 9分
(3)由题设得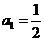 ,
, 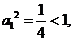
当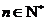 时,
时,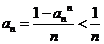 .
.
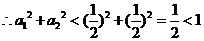 . …………………………12分
. …………………………12分
当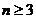 时有
时有
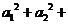
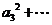
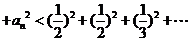
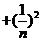
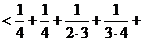 …
…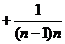
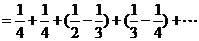
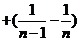
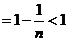 .
.
综上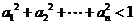 .…………………………… 14分
.…………………………… 14分
20.(本小题满分14分)解:(1)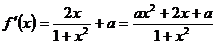 . ……1分
. ……1分
①当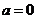 时,
时,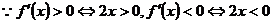 ,
,
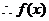 在
在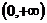 单调递增,在
单调递增,在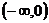 单调递减;…………3分
单调递减;…………3分
②当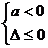 ,即
,即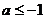 时,
时,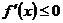 对
对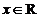 恒成立
恒成立
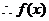 在
在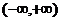 上单调递减; ……………………………………………… 5分
上单调递减; ……………………………………………… 5分
③当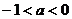 时,
时,
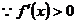
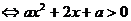
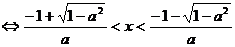
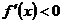
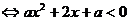
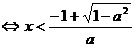 或
或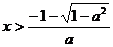
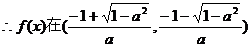 上单调递增,
上单调递增,
在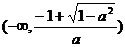 和
和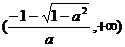 上单调递减; …………………… 7分
上单调递减; …………………… 7分
综上所述,当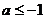 时,
时,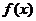 在
在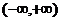 上单调递减,
上单调递减,
当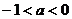 时,
时,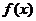 在
在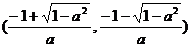 上单调递增,
上单调递增,
在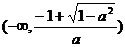 和
和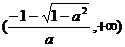 上单调递减.
上单调递减.
当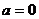 时,
时,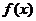 在
在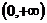 单调递增,在
单调递增,在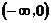 上单调递减. …………8分
上单调递减. …………8分
(2)由(1)知,当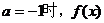 在
在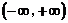 上单调递减,
上单调递减,
当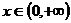 时,由
时,由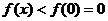 得
得 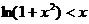 ……………………………10分
……………………………10分
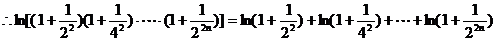
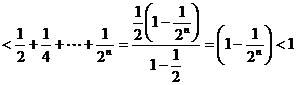
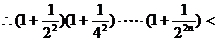
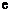 ……………………………14分
……………………………14分
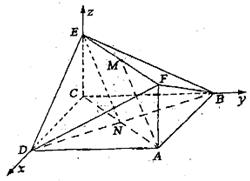
19.(本小题满分14分)解:(1)以直线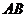 为
为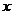 轴,线段
轴,线段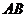 的中点为原点,
的中点为原点,
建立如图所示的平面直角坐标系,
则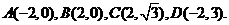 ……… 1分
……… 1分
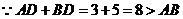 ,
,
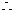 依题意,曲线段
依题意,曲线段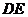 是以
是以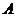 、
、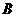 为左、右焦点,长轴长为
为左、右焦点,长轴长为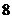 的椭圆的一部分.… 3分
的椭圆的一部分.… 3分
故曲线段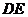 的方程为
的方程为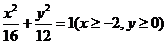 . …… 6分
. …… 6分
(2)设这样的直线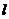 存在,由直线
存在,由直线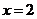 与曲线段
与曲线段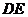 只有一个交点
只有一个交点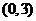 ,
,
知直线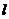 存在斜率,设直线
存在斜率,设直线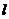 的方程为
的方程为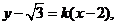 即
即 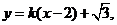
将其代入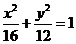 得
得
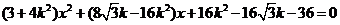 ① …………………… 9分
① …………………… 9分
设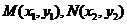 ,则由
,则由
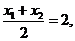 知
知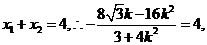 解得
解得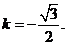 …………………12分
…………………12分
当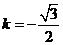 时,方程①化为:
时,方程①化为: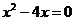 ,解得
,解得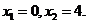
即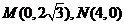 ,适合条件.
,适合条件.
故直线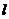 存在,其方程为
存在,其方程为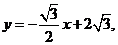 即
即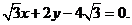 ……………… 14分
……………… 14分
18.解:方法一:(1)记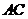 与
与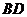 的交点为
的交点为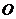 ,连接
,连接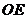 ,
,
 ∵
∵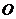 、
、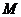 分别是
分别是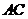 、
、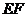 的中点,
的中点,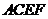 是矩形,
是矩形,
∴四边形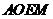 是平行四边形,∴
是平行四边形,∴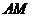 ∥
∥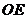 .
.
∵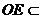 平面BDE,
平面BDE,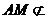 平面
平面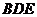 ,
,
∴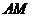 ∥平面
∥平面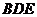 . ………………… 4分
. ………………… 4分
(2)在平面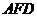 中过
中过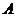 作
作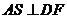 于
于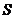 ,连结
,连结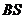 ,
,
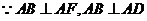 ,
, 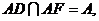 ∴
∴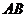 ⊥平面
⊥平面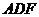 ,
,
∴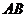 ⊥
⊥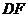 ,又
,又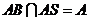
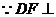 平面
平面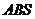
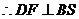 ,
,
∴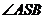 是二面角
是二面角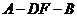 的平面角. ……………………………………… 6分
的平面角. ……………………………………… 6分
在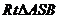 中,
中,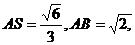 ∴
∴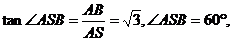
∴二面角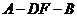 的大小为
的大小为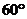 . ……………………………………………… 9分
. ……………………………………………… 9分
 (3)设
(3)设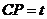 (
(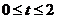 ),作
),作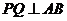 于Q,则
于Q,则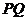 ∥
∥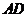 ,
,
∵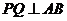 ,
,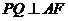 ,
,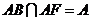 ,
,
∴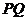 ⊥平面
⊥平面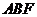 ,
,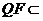 平面
平面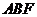 ,∴
,∴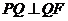 .
.
在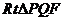 中,
中,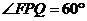 ,
,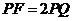 .
.
∵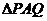 为等腰直角三角形,∴
为等腰直角三角形,∴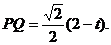
又∵Δ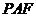 为直角三角形,∴
为直角三角形,∴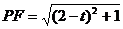 ,
,
∴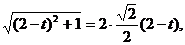
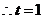 或
或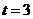 (舍去).
(舍去).
∴点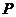 是
是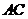 的中点. …………… 14分
的中点. …………… 14分
方法二:(1)建立如图所示的空间直角坐标系.设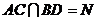 ,连接
,连接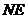 ,
,
则点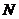 、
、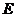 的坐标分别是(
的坐标分别是(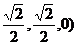 、
、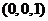 ,∴
,∴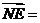 (
(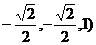 ,
,
又点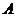 、
、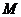 的坐标分别是(
的坐标分别是(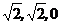 )、(
)、(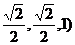 ,∴
,∴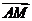 =(
=(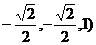
∴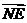 =
=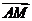 且
且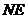 与
与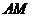 不共线,∴
不共线,∴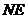 ∥
∥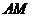 .
.
又∵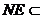 平面BDE,
平面BDE,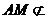 平面
平面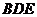 ,∴
,∴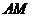 ∥平面
∥平面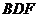 . ………………… 4分
. ………………… 4分
(2)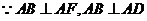 ,
,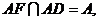 ∴
∴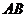 ⊥平面
⊥平面 .
.
 ∴
∴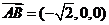 为平面
为平面 的法向量.
的法向量.
∵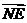
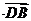 =(
=(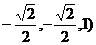 ·
·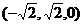 =0,
=0,
∴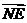 ·
·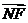 =(
=(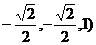 ·
·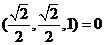 ,
,
得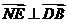 ,
,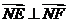 ∴
∴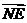 为平面
为平面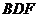 的法向量.
的法向量.
∴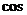 <
<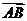 ,
,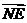 >
>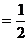 ,∴
,∴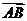 与
与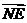 的夹角是
的夹角是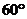 .
.
即所求二面角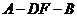 的大小是
的大小是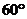 . ……………………………… 9分
. ……………………………… 9分
(3)设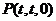
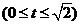 ,得
,得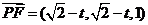 ,∴
,∴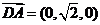 ,
,
 又∵
又∵ 和
和 所成的角是
所成的角是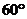 .
. 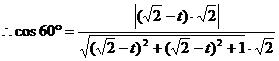 ,
,
解得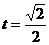 或
或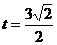 (舍去),即点
(舍去),即点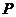 是
是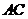 的中点.……14分
的中点.……14分
解:(1)
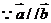 ,
,

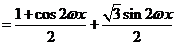
 .…… 4分
.…… 4分
由题意,函数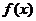 的最小正周期为
的最小正周期为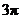 ,又
,又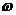 >0,
>0,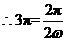
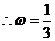 . ……………6分
. ……………6分
(2) 由(1)知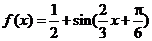 ,
,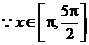 ,
,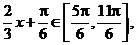
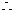 当
当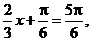 即
即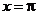 时,
时,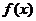 取得最大值
取得最大值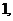 ……………………………… 9分
……………………………… 9分
当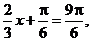 即
即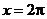 时,
时,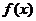 取得最小值
取得最小值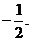 ………………………12分
………………………12分
17.解:(1)两次抽取的球的分值构成的有序数对共有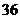 对,其中分值之和为
对,其中分值之和为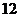 的有
的有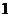 对,分值之和为
对,分值之和为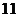 的有两对,分值之和为
的有两对,分值之和为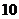 的有
的有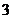 对,所以每位会员获奖的概率为
对,所以每位会员获奖的概率为
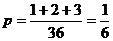 .……………………4分
.……………………4分
(2)设每位来宾抽奖后,休闲宾馆的获利的元数为随机变量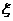 ,则
,则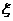 的可能取值为
的可能取值为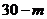 、
、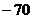 、
、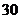 .………5分
.………5分
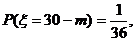
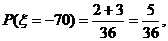
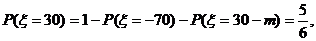 …8分
…8分
则宾馆获利的期望为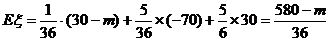 .
.
若这次活动会馆既不赔钱也不赚钱,则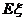 =0,即
=0,即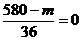 ,
,
所以,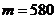 . ………………………………11分
. ………………………………11分
答:(1)每位会员获奖的概率为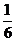 ;(2)
;(2)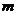 应为
应为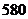 元. …………………………12分
元. …………………………12分
9. 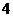 ; 10.
; 10. 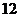 ; 11.
; 11. 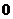 或
或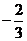 ; 12.
; 12. 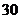 ; 13.
; 13. 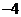 ; 14.
; 14. 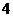 ; 15.
; 15. 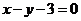 .
.
|
题次 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
答案 |
B |
C |
A |
C |
B |
C |
D |
D |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com