
5.设向量a与b的夹角为θ,a=(2,1),a+2b=(4,5),则cosθ等于
A.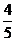 B.
B.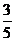 C.
C.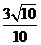 D.
D.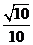
4.设p:f(x)=x3+2x2+mx+l在(-∞,+∞)内单调递增,q:m≥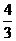 ,则p是q的
,则p是q的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.下列函数既是奇函数,又在区间[一1,1]上单调递减的是
A.f(x)=sinx B.f(x)=-|x+1|
C.f(x)=ln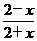 D.f(x)=
D.f(x)=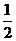 (
(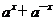 )
)
2.已知复数z=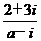 (a ∈R)是纯虚数,则a的值等于
(a ∈R)是纯虚数,则a的值等于
A.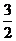 B.-
B.-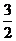 C.-
C.-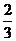 D.1
D.1
1.集合M={x||x-3|≤4},N={y|y=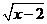 +
+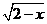 },则M∩N=
},则M∩N=
A.{0}
B.{2}
C.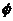 D.{x|2≤x≤7}
D.{x|2≤x≤7}
21.(本小题满分14分)
设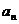 是关于
是关于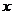 的方程
的方程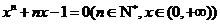 的根. 试证明:
的根. 试证明:
(1)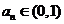 ;
;
(2)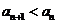 ;
;
(3)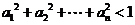 .
.
20.(本小题满分14分)
已知函数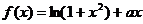 ,其中
,其中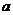 为不大于零的常数.
为不大于零的常数.
(1) 讨论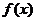 的单调性;
的单调性;
(2) 证明: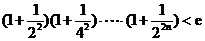 (
(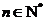 ,
,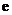 为自然对数的底数).
为自然对数的底数).
19.(本小题满分14分)
如图,在直角梯形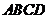 中,
中,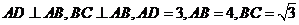 ,点
,点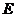 在线段
在线段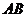 的延长线上.曲线段
的延长线上.曲线段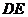 上任一点到
上任一点到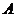 、
、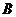 两点的距离之和都相等.
两点的距离之和都相等.
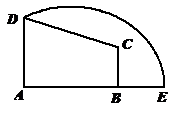 (1)建立适当的直角坐标系,求曲线段
(1)建立适当的直角坐标系,求曲线段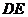 的方程;
的方程;
(2)试问:过点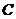 能否作一条直线
能否作一条直线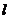 与曲线段
与曲线段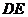 相交于两点
相交于两点
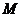 、
、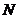 ,使得线段
,使得线段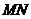 以C为中点?若能,则求直线
以C为中点?若能,则求直线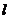 的方程;
的方程;
若不能,则说明理由.
18.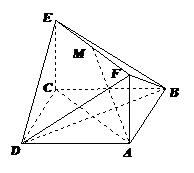 (本小题满分14分)
(本小题满分14分)
如图,已知正方形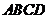 和矩形
和矩形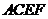 所在平面互相垂直,
所在平面互相垂直,
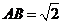 ,
,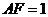 ,
,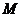 是线段
是线段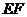 的中点.
的中点.
(1)求证: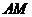 ∥平面
∥平面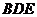 ;
;
(2)求二面角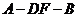 的大小;
的大小;
(3)试问:在线段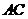 上是否存在一点
上是否存在一点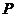 ,使得直线
,使得直线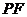 与
与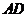 所成角为
所成角为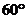 ?
?
17.(本小题满分12分)
某休闲会馆拟举行“五一”庆祝活动,每位来宾交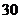 元的入场费,可参加一次抽奖活动. 抽奖活动规则是:从一个装有分值分别为
元的入场费,可参加一次抽奖活动. 抽奖活动规则是:从一个装有分值分别为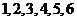 的六个相同小球的抽奖箱中,有放回的抽取两次,每次抽取一个球,规定:若抽得两球的分值之和为
的六个相同小球的抽奖箱中,有放回的抽取两次,每次抽取一个球,规定:若抽得两球的分值之和为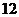 分,则获得价值为
分,则获得价值为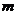 元的礼品;若抽得两球的分值之和为
元的礼品;若抽得两球的分值之和为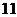 分或
分或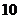 分,则获得价值为
分,则获得价值为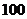 元的礼品;若抽得两球的分值之和低于
元的礼品;若抽得两球的分值之和低于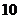 分,则不获奖.
分,则不获奖.
(1)求每位会员获奖的概率;
(2)假设这次活动会馆既不赔钱也不赚钱,则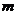 应为多少元?
应为多少元?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com