
1. [巩固1]bn=2n-1+2,Tn=2n+2n-1,[巩固2] (1)an=2n-1,bn=3n-1,(2)32007,
5.在解以数列为数学模型的应用题时,要选择好研究对象,即选择好以“哪一个量”作为数列的“项”,并确定好以哪一时刻的量为第一项;对较简单的问题可直接寻找“项”与“项数”的关系,对较复杂的问题可先研究前后项之间的关系(即数列的递推关系),然后再求通项。
[举例] 从盛满729升纯酒精的容器里倒出a升,然后用水填满,再倒出a升混合溶液,用水填满,这样继续进行,一共倒了6次,这时容器里还含有64升纯酒精,则a的值为 .
解析:记:倒了n次后容器里还含有an升纯酒精,则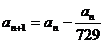 a
a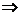
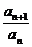 =
= ,
,
数列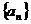 为等比数列,公比为
为等比数列,公比为 ,a1=729-a,∴
,a1=729-a,∴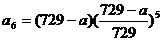
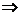 64×7295=(729-a )6,
64×7295=(729-a )6, 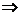 2×35=729-a
2×35=729-a 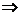 a=343。
a=343。
[巩固]在占地3250亩的荒山上建造森林公园,2000年春季植树100亩,以后每年春季植树面积都比上一年多植树50亩,直到荒山全部绿化为止.
(1) 到哪一年春季才能将荒山全部绿化完?
(2) 如果新植树木的每亩木材量为2m3,树木每年自然增长率为20%,到全部绿化完的那年春季,该森林公园的木材总量是多少?(精确到1m3,1.29≈1.56)
简答
4.与数列相关的不等式问题多用“放缩法”或数列的单调性解决。
[举例1]在数列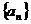 中,已知
中,已知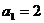 ,
,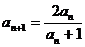 ,
,
(Ⅰ)证明数列{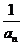 -1}是等比数列,并求数列
-1}是等比数列,并求数列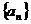 的通项公式;
的通项公式;
(Ⅱ)求证: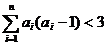
解析:(Ⅰ)留给读者自己完成(参看第2条[举例]②),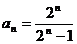 ;(Ⅱ)
;(Ⅱ)
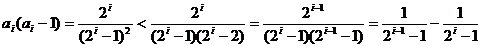 (
(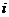 ≥2)
≥2)
∴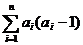 =2+
=2+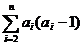 <2+1-
<2+1-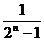 <3.
<3.
[巩固] 已知在数列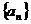 的前n和为Sn ,且对一切正整数n都有Sn=n2+
的前n和为Sn ,且对一切正整数n都有Sn=n2+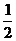 an,
an,
(Ⅰ)求证:an+1+
an=4n+2; (Ⅱ)求数列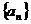 的通项公式;
的通项公式;
(Ⅲ)是否存在实数a,使不等式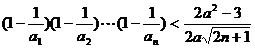 对一切正整数n都成立?若存在,求出a的取值范围;若不存在,请说明理由。
对一切正整数n都成立?若存在,求出a的取值范围;若不存在,请说明理由。
3. 应掌握数列求和的常用方法:应用公式(必须要记住几个常见数列的前n项和)、折项分组(几个数列的和、差)、裂项相消(“裂”成某个数列的相邻两项差后叠加)、错位相减(适用于一个等差数列和一个等比数列的对应项乘积构成的数列)、倒序相加等,要根据不同数列的特点合理选择求和方法(其中最重要、最常见的是裂项)。
[举例]①数列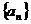 中,若
中,若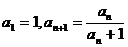 ,数列
,数列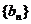 满足
满足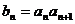 ,则数列
,则数列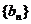 的前
的前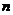 项和为
。
项和为
。
解析:求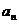 的过程请读者自己完成。
的过程请读者自己完成。 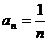
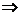
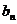 =
=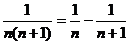 ,
,
∴数列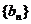 的前
的前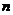 项和为:
项和为: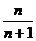 。一般地:通项为分式的数列求和多用“裂项”,“裂项”是“通分”的逆运算,可以先“裂开”再回头通分“凑”系数。
。一般地:通项为分式的数列求和多用“裂项”,“裂项”是“通分”的逆运算,可以先“裂开”再回头通分“凑”系数。
②已知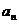 =
=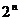 ,Sn为数列{
,Sn为数列{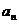 }的前n项和,
}的前n项和,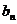 =nSn,求数列{
=nSn,求数列{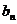 }的前n项和Tn;
}的前n项和Tn;
解析:Sn=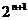 -2
-2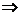
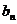 =n×
=n×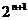 -2n, Tn=1×22+2×23+3×24+…+ n×
-2n, Tn=1×22+2×23+3×24+…+ n×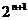 -2(1+2+3+…+n)
-2(1+2+3+…+n)
(视数列{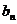 }的前n项和为两个数列的前n项和的差,此即“分组求和”)记:
}的前n项和为两个数列的前n项和的差,此即“分组求和”)记:
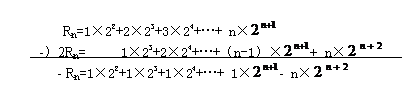 Rn=1×22+2×23+3×24+…+ n×
Rn=1×22+2×23+3×24+…+ n×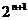 ,求Rn用“错位相减”法:
,求Rn用“错位相减”法:
- Rn=2n+2-4-n×2n+2=-(n-1) 2n+2-4,∴Rn=(n-1) 2n+2+4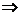 Tn=(n-1) 2n+2+4-n(n+1)。
Tn=(n-1) 2n+2+4-n(n+1)。
注:“错位相减”法在中学数学中除推倒等比数列的求和公式外就仅此一用。“相减”后的n+1项中,“掐头去尾”中间的n-1项成等比数列。
③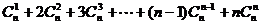 =
=
解析:S=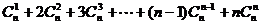 =
=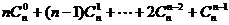
用“倒序相加”:得2S=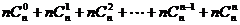 =n2n, ∴S=n2n-1 。
=n2n, ∴S=n2n-1 。
[巩固]设数列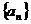 是公差不为零的等差数列,其前
是公差不为零的等差数列,其前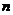 项之和为
项之和为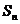 ,已知
,已知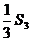 与
与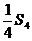 的等比中项为
的等比中项为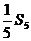 ,且
,且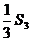 与
与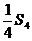 的等差中项为1。(1)求数列
的等差中项为1。(1)求数列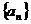 的通项公式;
的通项公式;
(2)若数列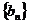 的前项之和为
的前项之和为 ,其中
,其中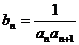 ,问是否存在实数M,使得
,问是否存在实数M,使得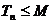 对任意正整数
对任意正整数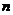 都成立?若存在,试求出实数M的范围;若不存在,试说明理由。
都成立?若存在,试求出实数M的范围;若不存在,试说明理由。
2.形如: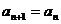 +
+ 的递推数列,求通项时先“移项”得
的递推数列,求通项时先“移项”得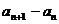 =
= 后,再用叠加(消项)法;形如:
后,再用叠加(消项)法;形如: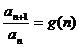 的递推数列,求通项用连乘(约项)法;形如:an+1= qan+p (a1=a,p、q为常数)的递推数列求通项公式可以逐项递推出通项(在递推的过程中把握规律)或用待定系数法构造等比数列(公比为q);形如:
的递推数列,求通项用连乘(约项)法;形如:an+1= qan+p (a1=a,p、q为常数)的递推数列求通项公式可以逐项递推出通项(在递推的过程中把握规律)或用待定系数法构造等比数列(公比为q);形如: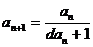 (
(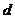 为常数)的递推数列求通项,先“取倒数”,可得数列{
为常数)的递推数列求通项,先“取倒数”,可得数列{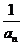 }是等差数列(公差为
}是等差数列(公差为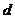 )。
)。
[举例]①已知数列{an}满足a1=1,an+1=an+2n-1,则a10 ;
解析:an+1-an=2n-1,分别取n=1,2,…9,叠加得:a10-a1=(2+22+…+29)-9=210-11
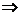 a10=210-10.
a10=210-10.
②若数列{an}满足a1=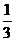 ,
,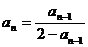 (n≥2), 则an=
;
(n≥2), 则an=
;
解析:“取倒数”得: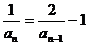 (n≥2),记数列{
(n≥2),记数列{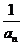 +
+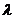 }为等比数列,且公比为2,
}为等比数列,且公比为2,
(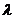 为常数),则
为常数),则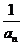 +
+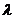 =2(
=2(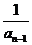 +
+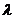 )
)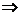
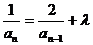 (n≥2),可见
(n≥2),可见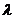 =-1,而
=-1,而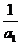 -1=2
-1=2
∴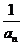 -1=2n,
-1=2n, 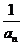 =2n+1, an=
=2n+1, an=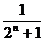 。注:(ⅰ)
。注:(ⅰ)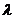 有时能够看、猜、试出来,未必非要“待定系数”。(ⅱ)数列{
有时能够看、猜、试出来,未必非要“待定系数”。(ⅱ)数列{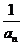 +
+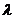 }为等比数列,其首项是
}为等比数列,其首项是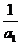 +
+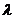 而不是a1,同样,通项是
而不是a1,同样,通项是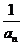 +
+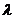 而不是an,这是很容易出错的一个地方。(ⅲ)若递推关系变为an+1= qan+pn,则
而不是an,这是很容易出错的一个地方。(ⅲ)若递推关系变为an+1= qan+pn,则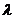 也相应变为
也相应变为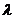 pn,其他做法不变。
pn,其他做法不变。
③已知数列{an}满足:a1+2a2+3a3+…+nan=an+1且a2=2, 则an 。
解析:“降标”得a1+2a2+3a3+…+(n-1)an-1=an,(n≥2)
作差得(n+1)an=an+1(n≥2)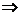
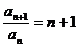 (n≥2)分别取n=2,3,…,n-1, 连乘得:
(n≥2)分别取n=2,3,…,n-1, 连乘得:
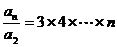 ,又a2=2得an=n! (n≥2)而a1=a2,∴an=
,又a2=2得an=n! (n≥2)而a1=a2,∴an=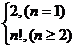 。
。
[提高]某顾客购买一件售价为1万元的商品,拟采用分期付款的方式在一年内分12次等额付清,即在购买后1个月第一次付款,以后每月付款一次,若商场按0.8%的月利率受取利息(计复利),则该顾客每月付款的数额为______
1. 遇到数列前n项和Sn与通项an的关系的问题应利用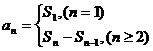
使用这个结论的程序是:写出Sn的表达式,再“后退”一步(降标)得Sn-1的表达式,作差;得an的表达式。注意:n≥2的要求切不可疏忽!若Sn的表达式无法写出,亦可将an表示成Sn-Sn-1,得到一个关于Sn的递推关系后,进一步求解。
[举例1] 数列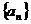 的前n项和
的前n项和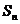 =an+b,(a
=an+b,(a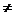 0, 且a
0, 且a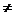 1),则数列
1),则数列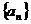 成等比数列的充要条件是__________
成等比数列的充要条件是__________
解析:降标得: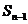 =an-1+b, (n≥2),作差得:an=an- an-1= an-1(a-1), (n≥2)
=an-1+b, (n≥2),作差得:an=an- an-1= an-1(a-1), (n≥2)
再“升标”得:an+1= an(a-1);∴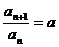 ,(n≥2),∴数列
,(n≥2),∴数列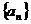 成等比数列的充要条件是:
成等比数列的充要条件是:
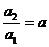 ,即
,即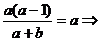 b= –1。
b= –1。
[举例2]数列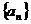 中,a1=1,Sn为数列{
中,a1=1,Sn为数列{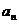 }的前n项和,n≥2时
}的前n项和,n≥2时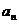 =3Sn,则Sn= 。
=3Sn,则Sn= 。
解析:思路一:同[举例1]得:an –an-1=3an (n≥3)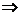
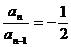 (n≥3) ∴数列
(n≥3) ∴数列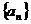 从第二项开始成等比数列(注意:不是从第三项开始),又a2=3(a1+a2)得a2=
从第二项开始成等比数列(注意:不是从第三项开始),又a2=3(a1+a2)得a2=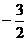 ,∴n≥2时
,∴n≥2时
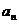 = a2qn-2=(
= a2qn-2=(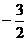 )(
)(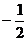 )n-2(这个地方极容易出错),即
)n-2(这个地方极容易出错),即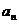 =
=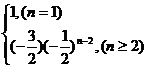
∴Sn=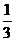
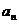 =
=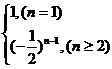 ,注意到n=1和n≥2可以统一,∴Sn=
,注意到n=1和n≥2可以统一,∴Sn=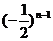 。(冗长烦琐,步步荆棘!)思路二:要求的不是
。(冗长烦琐,步步荆棘!)思路二:要求的不是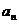 而是Sn,可以考虑在
而是Sn,可以考虑在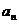 =3Sn中用Sn-Sn-1代换
=3Sn中用Sn-Sn-1代换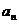 (体现的是“消元”的思想,思路一是加减消元,消去Sn;思路二是代入消元,消去
(体现的是“消元”的思想,思路一是加减消元,消去Sn;思路二是代入消元,消去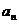 )得:Sn-Sn-1=3Sn,
)得:Sn-Sn-1=3Sn,
(n≥2),即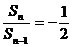 ,(n≥2),又S1=1,∴Sn =
,(n≥2),又S1=1,∴Sn =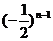 。
。
[巩固1]数列{an}的前n项和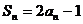 ,数列{bn}满足:
,数列{bn}满足: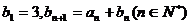 .
.
(Ⅰ)证明数列{an}为等比数列;(Ⅱ)求数列{bn}的前n项和Tn。
[巩固2]等差数列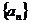 的首项a1=1,公差d>0,且第二项、第五项、第十四项分别为等比数列
的首项a1=1,公差d>0,且第二项、第五项、第十四项分别为等比数列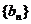 的第二项、第三项、第四项
的第二项、第三项、第四项
(1)
求数列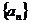 与
与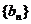 的通项公式;
的通项公式;
(2) 设数列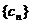 对任意整数n都有
对任意整数n都有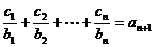 成立,
成立,
求c1+c2+…+c2007的值.
22.(本题满分14分)
已知实数a≥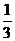 ,函数y=ex-ax区间[-ln3,o)上的增函数,设函数f(x)=ax3-
,函数y=ex-ax区间[-ln3,o)上的增函数,设函数f(x)=ax3-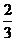 x
x
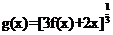 。
。
(I)求a的值并写出g(x)的表达式;
(Ⅱ)求证:当x>o时, 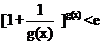
(Ⅲ)设an=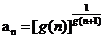 ,其中n∈N+,问数列{
,其中n∈N+,问数列{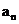 }中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由.
}中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由.




21.(本题满分1 2分)
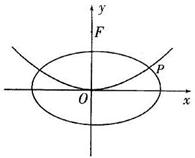 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆 C2:
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆 C2: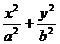 =l(a>b>o)的离心率e=
=l(a>b>o)的离心率e=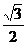 ,c1与c2在第一象限的交点为p(
,c1与c2在第一象限的交点为p(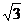 ,
,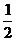 ).
).
(I)求抛物线C1及椭圆C2的方程;
(Ⅱ)已知直线l:y=kx+t(k≠0,t>0)与椭圆C2交于不同两点A、B,
点m满足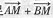 =0,直线FM的斜率为k1,试证明k·k1>-
=0,直线FM的斜率为k1,试证明k·k1>-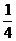 。
。
1 7.(本题满分1 2分)
已知钝角△ABC中,角A、B、c的对边分别为a、b、c,且(在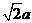 一c)cosB=bcosC.
一c)cosB=bcosC.
(I)求角B的大小;
(Ⅱ)设向量m=(cos2A+1,cosA),n=(1,-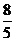 ),且m⊥n,求tan(
),且m⊥n,求tan(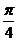 +A)的值.
+A)的值.
1 8.(本题满分1 2分)
已知数列{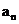 }的前n项积Tn=a1·a2·a3·…·an=
}的前n项积Tn=a1·a2·a3·…·an=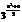 ;数列{
;数列{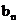 }为等差数列,且公差d>0,bl+b2+b3=l5.
}为等差数列,且公差d>0,bl+b2+b3=l5.
(I)求数列{an}的通项公式;
(Ⅱ)若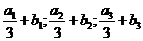 成等比数列,求数列{
成等比数列,求数列{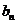 }的前n项和
}的前n项和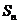 .
.
1 9.(本题满分1 2分)
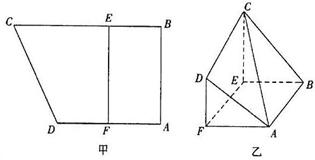
如图甲,直角梯形ABCD中,AB ⊥AD,AD∥BC,F为AD中点,E在BC上,且EF∥AB,已知AB=AD=CE=2,现沿EF把四边形CDFE折起如图乙,使平面CDFE⊥平面ABEF.
(I)求证:AD∥平面BCE;
(Ⅱ)求CD与平面ABC所成角的正弦值
20.(本题满分1 2分)
某工厂生产一种零件,该零件有甲、乙两项技术指标需要检验,设两项技术指标检验互不影响,经研究甲项指标达标率为2/3,乙项指标达标率为3/4.规定:两项指标都达标的零件为一等品,其中一项指标不达标为二等品,两项均不达标的为次品.已知生产一个一等品、二等品的利润分别为500元、200元,出现一个次品亏损400元.
(I)求生产一个零件的平均利润;
(Ⅱ)若该工厂某时段生产了5个零件,记该5个零件中一等品的个数为X,求p(X≥2)及E(X),D(X).
16.设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x-1),已知:当x∈[0,1]时f(x)=(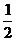 )1-x,则
)1-x,则
①2是函数f(x)的周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④当x∈[3,4]时,f(x)=(
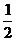 )x-3.
)x-3.
其中所有正确命题的序号是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com