
6.在等差数列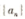 中,若
中,若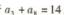 .则
.则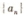 的前IO项和
的前IO项和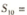
(A)70 (B)80 (C)90 (D)IOO
5.某篮球运动员在三分线投篮的命准率为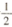 ,他投篮5次,恰好投准3次的概率为
,他投篮5次,恰好投准3次的概率为
(A) 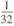 (B)
(B) 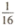 ( C)
( C) 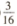 (D)
(D) 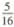
4.下列四个数中,最大的一个是
(A) 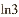 (B)
(B) 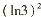 (C)
(C) 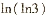 (D)
(D) 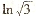
3.在△ABC中,若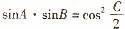 ,则△ABC的形状为
,则△ABC的形状为
(A)直角三角形 (B)等边三角形 (c)等腰三角形 (D)等腰直角三角形
2. 函数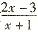 的反函数为
的反函数为
(A)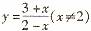 (B)
(B)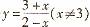 (C)
(C)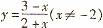 (D)
(D)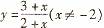
1.已知集合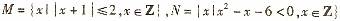 .则
.则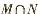 =
=
(A) 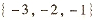 (B)
(B) 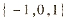 (C)
(C) 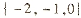 (D)
(D) 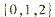
3.电场力做的功等于电势能的变化量。
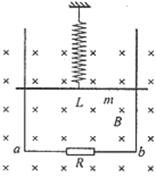 题型6.(功能关系在电磁感应中的应用)两根足够长的光滑导轨竖直放置,间距为L ,底端接阻值为R 的电阻。将质量为m的金属棒悬挂在一个固定的轻弹簧下端,金属棒和导轨接触良好,导轨所在平面与磁感应强度为B 的匀强磁场垂直,如图所示。除电阻R 外其余电阻不计。现将金属棒从弹簧原长位置由静止释放.则
题型6.(功能关系在电磁感应中的应用)两根足够长的光滑导轨竖直放置,间距为L ,底端接阻值为R 的电阻。将质量为m的金属棒悬挂在一个固定的轻弹簧下端,金属棒和导轨接触良好,导轨所在平面与磁感应强度为B 的匀强磁场垂直,如图所示。除电阻R 外其余电阻不计。现将金属棒从弹簧原长位置由静止释放.则
A.释放瞬间金属棒的加速度等于重力加速度g
B.金属棒向下运动时,流过电阻R 的电流方向为a→b
C.金属棒的速度为v时.所受的安培力大小为F =
D.电阻R 上产生的总热量等于金属棒重力势能的减少
解析:在释放的瞬间,速度为零,不受安培力的作用,只受到重力,A对。由右手定则可得,电流的方向从b到a,B错。当速度为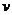 时,产生的电动势为
时,产生的电动势为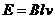 ,受到的安培力为
,受到的安培力为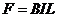 ,计算可得
,计算可得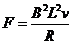 ,C对。在运动的过程中,是弹簧的弹性势能、重力势能和内能的转化,D错。
,C对。在运动的过程中,是弹簧的弹性势能、重力势能和内能的转化,D错。
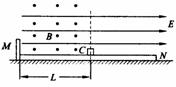
题型7.(功能关系在混合场内的应用)如图所示,MN是一固定在水平地面上足够长的绝缘平板(左侧有挡板),整个空间有平行于平板向右、场强为E=2N/C的匀强电场,在板上C点的左侧有一个垂直于纸面向外、磁感应强度为B=1T的匀强磁场,一个质量为m=4×10-3kg、带负电的小物块,带电量q=10-2C,从C点由静止开始向左先做加速运动再做匀速运动. 当物体碰到左端挡板后被弹回,若在碰撞瞬间将电场改为竖直向下,大小不变. 小物块返回时在磁场中恰做匀速运动,已知平板MC部分的长度为L=5m,物块与平板间的动摩擦因数为μ=0.2,求:
 (1)小物块向左运动过程中克服摩擦力做的功Wf;
(1)小物块向左运动过程中克服摩擦力做的功Wf;
(2)小物块与左端挡板碰撞过程损失的机械能△E;
(3)小物块从与 左挡板碰后到最终静止所用时间t;
(4)整个过程中由于摩擦产生的热量Q.
解析:设小物块向左匀速运动时的速度大小为v1,由平衡条件有
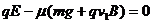 ①
①
设小物块在向左运动过程中克服摩擦力做的功为W,由动能定理有
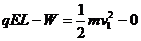 ②
②
由①②式解得 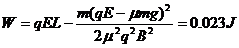 ③
③
(2)设小物块返回时在磁场中匀速运动的速度大小为v2,与右端挡板碰撞过程损失机构能为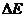 ,则有
,则有 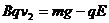 ④
④
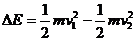 ⑤
⑤
由③⑤⑥式解得 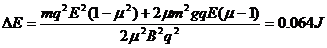 ⑥
⑥
(3)小物块由M到C匀速运动,时间为
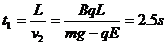 ⑦
⑦
小物块由C到静止匀减速运动,
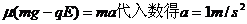 ⑧
⑧
时间为 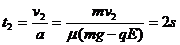 ⑨
⑨
总时间为 t=t1+t2=4.5s ⑩
(4)对全过程,由能量守恒定律有 11
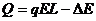 12
12
(或 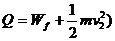
由⑤⑧式解得 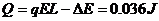 13
13
评分标准:①式2分,其余各1分,共14分

2.电场力做功与路径无关,W=qU。
题型1.(功能关系的应用)从地面竖直上抛一个质量为m的小球,小球上升的最大高度为H。设上升过程中空气阻力为F恒定。则对于小球上升的整个过程,下列说法错误的是(
A. 小球动能减少了mgH
B. 小球机械能减少了FH
C. 小球重力势能增加了mgH
D. 小球加速度大于重力加速度g
解析:由动能定理可知,小球动能的减小量等于小球克服重力和阻力F做的功 为(mg+F)H,A错误;小球机械能的减小等于克服阻力F做的功,为FH,B正确;小球重力势能的增加等于小球小球克服重力做的功,为mgH,C正确;小球的加速度
为(mg+F)H,A错误;小球机械能的减小等于克服阻力F做的功,为FH,B正确;小球重力势能的增加等于小球小球克服重力做的功,为mgH,C正确;小球的加速度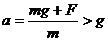 ,D正确。
,D正确。
规律总结:功是能量转化的量度,有以下几个功能关系需要理解并牢记
⑴重力做功与路径无关,重力的功等于重力势能的变化
⑵滑动摩擦力(或空气阻力)做的功与路径有关,并且等于转化成的内能
⑶合力做功等于动能的变化
⑷重力(或弹力)以外的其他力做的功等于机械能的变化
题型2.(功率及机车启动问题)
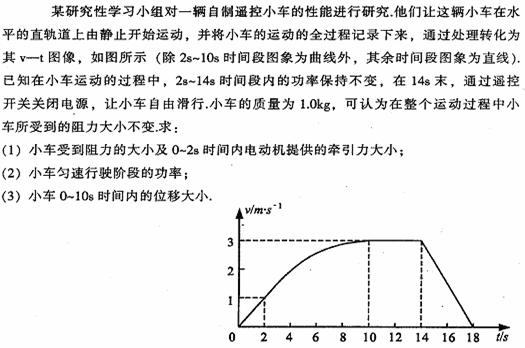

审题指导:1.在汽车匀加速启动时,匀加速运动刚结束时有两大特点
⑴牵引力仍是匀加速运动时的牵引力,即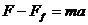 仍满足
仍满足
⑵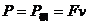
2.注意匀加速运动的末速度并不是整个运动过程的最大速度
题型3.(动能定理的应用)如图所示,竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成,AB恰与圆弧CD在C点相切,轨道固定在水平面上。一个质量为m的小物块(可视为质点)从轨道的A端以初动能E冲上水平轨道AB,沿着轨道运动,由DC弧滑下后停在水平轨道AB的中点。已知水平轨道AB长为L。求:
(1)小物块与水平轨道的动摩擦因数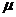

(2)为了保证小物块不从轨道的D端离开轨道,圆弧轨道的半径R至少是多大?
(3)若圆弧轨道的半径R取第(2)问计算出的最小值,增大小物块的初动能,使得小物块冲上轨道后可以达到最大高度是1.5R处,试求物块的初动能并分析物块能否停在水平轨道上。如果能,将停在何处?如果不能,将以多大速度离开水平轨道?
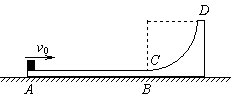
解析:(1)小物块最终停在AB的中点,在这个过程中,由动能定理得
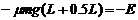
得 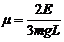
(2)若小物块刚好到达D处,速度为零,同理,有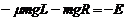
解得CD圆弧半径至少为 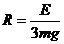
(3)设物块以初动能E′冲上轨道,可以达到的最大高度是1.5R,由动能定理得
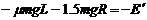
解得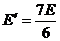
物块滑回C点时的动能为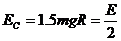 ,由于
,由于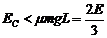 ,故物块将停在轨道上
,故物块将停在轨道上
设到A点的距离为x,有 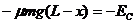
解得 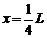
即物块最终停在水平滑道AB上,距A点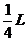 处。
处。
规律总结:应用动能定理要比动力学方法方便、简洁。只有应用动力学方法可以求解的匀变速直线运动问题,一般应用动能定理都可以求解。尽管动能定理是应用动力学方法推导出来的,但它解决问题的范围更广泛。
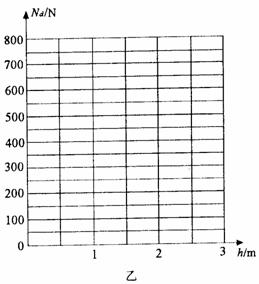
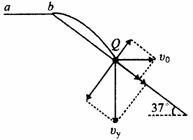
题型4.(综合问题)滑板运动是一项陆地上的“冲浪运动”,滑板运动员可在不同的滑坡上滑行,做出各种动作给人以美的享受。如图甲所示,abcdef为同一竖直平面上依次平滑连接的滑行轨道,其中ab段水平,H=3m,bc段和cd段均为斜直轨道,倾角θ=37º,de段是一半径R=2.5m的四分之一圆弧轨道,o点为圆心,其正上方的d点为圆弧的最高点,滑板及运动员总质量m=60kg,运动员滑经d点时轨道对滑板支持力用Nd表示,忽略摩擦阻力和空气阻力,取g=10m/s2,sin37º=0.6,
cos37º=0.8。除下述问(3)中运动员做缓冲动作以外,均可把滑板及运动员视为质点。
(1)运动员从bc段紧靠b处无初速滑下,求Nd的大小;
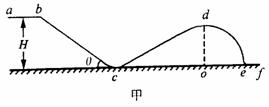
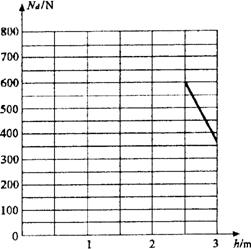
(2)运动员逐渐减小从bc上无初速下滑时距水平地面的高度h,请在图乙的坐标图上作出Nd-h图象(只根据作出的图象评分,不要求写出计算过程和作图依据);
(3)运动员改为从b点以υ0=4m/s的速度水平滑出,落在bc上时通过短暂的缓冲动作使他只保留沿斜面方向的速度继续滑行,则他是否会从d点滑离轨道?请通过计算得出结论
解析:解:(1)从开始滑下至d点,由机械能守恒定律得
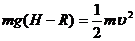 ①(1分)
①(1分)
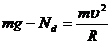 ②(1分)
②(1分)
由①②得: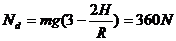 ③(1分)
③(1分)
(2)所求的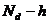 图象如图所示(3分)
图象如图所示(3分)
(图线两个端点画对各得1分,图线为直线得1分)
(3)当以 从b点水平滑出时,运动员做平抛运动落在Q点,如图所示。设Bq=
从b点水平滑出时,运动员做平抛运动落在Q点,如图所示。设Bq=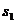 ,则
,则
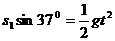 ④(1分)
④(1分)
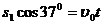 ⑤(1分)
⑤(1分)
由④⑤得
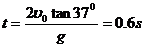 ⑥(1分)
⑥(1分)
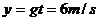 ⑦(1分)
⑦(1分)
在Q点缓冲后
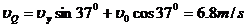 ⑧(1分)
⑧(1分)
从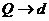
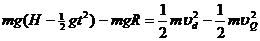 ⑨(1分)
⑨(1分)
运动员恰从d点滑离轨道应满足: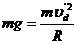 ⑩(1分)
⑩(1分)
由⑨⑩得
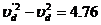 即
即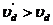 ⑩(1分)
⑩(1分)
可见滑板运动员不会从圆弧最高点d滑离轨道。(1分)
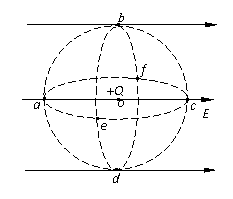 题型5.(功能关系在电场中的应用)如图所示匀强电场E的区域内,在O点处放置一点电荷 +Q, a、b、c、d、e、f为以O点为球心的球面上的点,aecf平面与电场平行,bedf平面与电场垂直,则下列说法中正确的是
题型5.(功能关系在电场中的应用)如图所示匀强电场E的区域内,在O点处放置一点电荷 +Q, a、b、c、d、e、f为以O点为球心的球面上的点,aecf平面与电场平行,bedf平面与电场垂直,则下列说法中正确的是
A.b、d两点的电场强度相同
B.a点的电势等于f点的电势
C.点电荷+q在球面上任意两点之间移动时,电场力一定做功
D.将点电荷+q在球面上任意两点之间移动,从球面上a点移动到c点的电势能变化量一定最大
解析:由于点电荷+Q在b、d两点的场强方向分别向上和向下,b、d两点的场强大小相同,方向不同,A错;a点和f点位于+Q形成电场的等势面上,但若把一电荷从a点移动到f点,电场E要对电荷做功,B错;当点电荷+q在bedf面上任意两点间移动时,电场力不做功,C错;球面上相距最远的点(沿场强E的方向)是ac,电场E对其做功最大,电势能的变化量最大。
规律总结:1.在等势面上移动电荷是,电场力不做功。
此专题复习时,可以先让学生完成相应的习题,在精心批阅之后以题目带动知识点,进行适当提炼讲解。这一专题的知识点高考要求普遍较高,属于必考知识点。二轮复习时还是要稳扎稳打,从基本规律,基本解题步骤出发再进行提升。因为这部分的综合题较多,功和能仅仅是在解题中应用的物理规律而以。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com