
1.1.2集合间的基本关系
练习(第7页)
2.解:(1)因为方程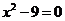 的实数根为
的实数根为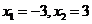 ,
,
所以由方程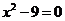 的所有实数根组成的集合为
的所有实数根组成的集合为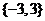 ;
;
(2)因为小于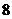 的素数为
的素数为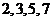 ,
,
所以由小于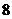 的所有素数组成的集合为
的所有素数组成的集合为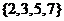 ;
;
(3)由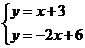 ,得
,得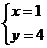 ,
,
即一次函数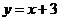 与
与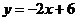 的图象的交点为
的图象的交点为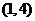 ,
,
所以一次函数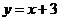 与
与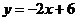 的图象的交点组成的集合为
的图象的交点组成的集合为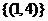 ;
;
(4)由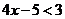 ,得
,得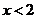 ,
,
所以不等式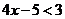 的解集为
的解集为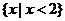 .
.
2.试选择适当的方法表示下列集合:
(1)由方程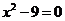 的所有实数根组成的集合;
的所有实数根组成的集合;
(2)由小于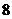 的所有素数组成的集合;
的所有素数组成的集合;
(3)一次函数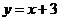 与
与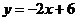 的图象的交点组成的集合;
的图象的交点组成的集合;
(4)不等式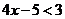 的解集.
的解集.
1.(1)中国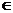
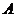 ,美国
,美国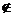
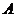 ,印度
,印度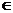
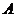 ,英国
,英国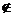
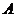 ;
;
中国和印度是属于亚洲的国家,美国在北美洲,英国在欧洲.
(2)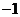
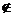
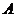
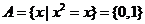 .
.
(3)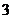
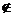
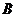
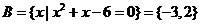 .
.
(4)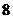
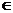
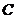 ,
,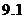
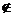
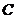
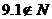 .
.
1.用符号“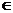 ”或“
”或“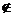 ”填空:
”填空:
(1)设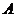 为所有亚洲国家组成的集合,则:中国_______
为所有亚洲国家组成的集合,则:中国_______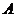 ,美国_______
,美国_______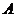 ,
,
印度_______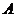 ,英国_______
,英国_______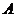 ;
;
(2)若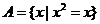 ,则
,则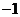 _______
_______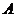 ;
;
(3)若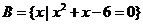 ,则
,则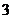 _______
_______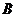 ;
;
(4)若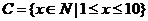 ,则
,则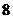 _______
_______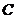 ,
,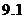 _______
_______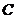 .
.
1.1.1集合的含义与表示
练习(第5页)
1.1集合
5.圆的参数方程的本质是sin2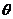 + cos2
+ cos2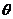 =1。参数方程的重要用途是设圆上一点的坐标时,可以减少一个变量,或者说坐标本身就已经体现出点在圆上的特点了,而无需再借助圆的方程来体现横纵坐标之间的关系。
=1。参数方程的重要用途是设圆上一点的坐标时,可以减少一个变量,或者说坐标本身就已经体现出点在圆上的特点了,而无需再借助圆的方程来体现横纵坐标之间的关系。
[举例]已知圆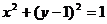 上任意一点P(x、y)都使不等式x+y+m³0成立,则m的取值范围是:A .[
上任意一点P(x、y)都使不等式x+y+m³0成立,则m的取值范围是:A .[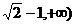 B
B 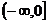 C (
C (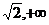 )
D
)
D 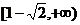 ( )
( )
解析:不等式x+y+m³0恒成立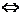 m³ -(x+y)恒成立,以下求-(x+y)的最大值:
m³ -(x+y)恒成立,以下求-(x+y)的最大值:
记x= cos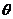 、y=1+
sin
、y=1+
sin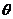 ,-(x+y)= -( cos
,-(x+y)= -( cos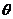 +1+ sin
+1+ sin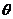 )= -1-
)= -1-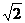 sin(
sin(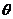 +
+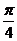 )≤-1+
)≤-1+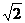 ,选A。
,选A。
[巩固1] 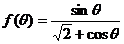 的最大值为
。
的最大值为
。
[巩固2]在⊿ABC中,已知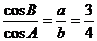 ,c=10,P是⊿ABC的内切圆上一点,则PA2+PB2
,c=10,P是⊿ABC的内切圆上一点,则PA2+PB2
+PC2的最大值为
[迁移]动点P,Q坐标分别为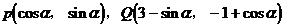 ,(
,(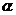 是参数),则|PQ|的最大值与最小值的和为 .
是参数),则|PQ|的最大值与最小值的和为 .
4.判断两圆的位置关系用圆心距与它们半径和、差的大小。⊙M、⊙N的半径分别为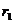 、
、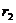 ,
,
|MN|>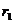 +
+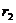
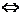 外离,|MN|=
外离,|MN|=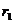 +
+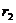
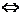 外切,|
外切,|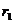 -
-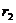 |<|MN|<
|<|MN|<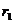 +
+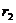
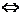 相交,此时,若⊙M:
相交,此时,若⊙M:
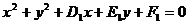 ,⊙N:
,⊙N: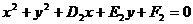 ,过两圆交点的圆(系)的方程为:
,过两圆交点的圆(系)的方程为: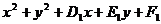 +
+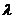 (
(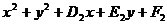 )=0(⊙N除外)。
)=0(⊙N除外)。
特别地:当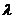 = -1时,该方程表示两圆的公共弦。连心线垂直平分公共弦。|MN|=|
= -1时,该方程表示两圆的公共弦。连心线垂直平分公共弦。|MN|=|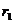 -
-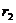 |
|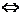 内切,|MN|<|
内切,|MN|<|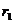 -
-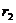 |
|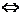 内含。
内含。
[举例1]已知两圆O1:x2+y2=16,O2:(x-1)2+(y+2)2=9,两圆公共弦交直线O1O2于M点,则O1分有向线段MO2所成的比λ= ( )
A.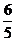 B.
B.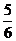 C.-
C.-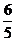 D.-
D.-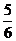
解析:直线O1 O2:y= -2x,两圆公共弦:x-2y=6,于是有:M(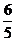 ,
,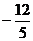 ),有定比分点坐标公式不难得到λ的值,选C。
),有定比分点坐标公式不难得到λ的值,选C。
[举例2] 若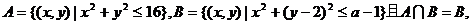
则a的取值范围是 ( )
A.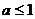 B.
B.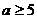 C.
C.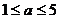 D.
D.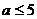
解析:集合A、B分别表示两个圆面(a=1时集B表示一个点),A∩B=B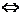 B
B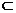 A,即两圆内含;有两圆圆心分别为原点和(0,2),半径分别为4和
A,即两圆内含;有两圆圆心分别为原点和(0,2),半径分别为4和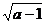 ,于是有:2≤4-
,于是有:2≤4-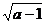 ,解得:
,解得: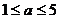 ,选C。
,选C。
[巩固1]圆心在直线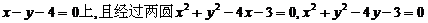 的交点的圆的方程为 ( )
的交点的圆的方程为 ( )
A.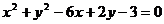 B.
B.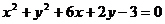
C.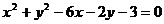 D.
D.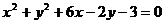
[巩固2]若圆(x-a)2+(y-b)2=6始终平分圆x2+y2+2x+2y-3=0的周长,则动点M(a,b)的轨迹方程是
A.a2+b2-2a-2b+1=0 B.a2+b2+2a+2b+1=0
C.a2+b2-2a+2b+1=0 D.a2+b2+2a-2b+1=0
[迁移]与圆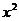 +
+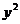
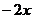 =0外切且与
=0外切且与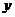 轴相切的动圆圆心的轨迹方程为
。
轴相切的动圆圆心的轨迹方程为
。
3.涉及直线与圆的位置关系的问题,宜用圆心到直线的距离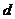 来研究。
来研究。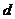 =
=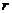 (
(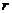 为圆的半径)
为圆的半径)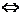 直线与圆相切;过圆x2+y2=r2上一点M(x0,y0)的切线方程为x0x+y0y=r2;过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点A、B连线的直线方程为x0x+y0y=r2。过⊙A外一点P作圆的切线PQ(Q为切点),则|PQ|=
直线与圆相切;过圆x2+y2=r2上一点M(x0,y0)的切线方程为x0x+y0y=r2;过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点A、B连线的直线方程为x0x+y0y=r2。过⊙A外一点P作圆的切线PQ(Q为切点),则|PQ|=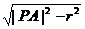 。
。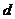 <
<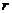
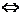 直线与圆相交,弦长|AB|=2
直线与圆相交,弦长|AB|=2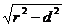 ;过直线A
;过直线A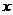 +B
+B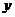 +C=0与圆:
+C=0与圆: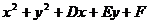 =0的交点的圆系方程:
=0的交点的圆系方程: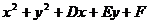 +
+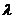 (A
(A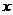 +B
+B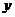 +C)=0
。
+C)=0
。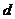 >
>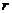
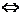 直线与圆相离,圆周上的点到直线距离的最小值为
直线与圆相离,圆周上的点到直线距离的最小值为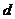 -
-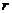 ,最大值为
,最大值为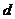 +
+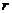 。
。
[举例1] 从直线x-y+3=0上的点向圆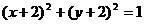 引切线,则切线长的最小值是
引切线,则切线长的最小值是
A.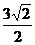 B.
B.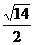 C.
C.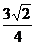 D.
D. 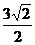 -1
-1
解析:圆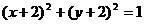 的圆心A(-2,-2),直线x-y+3=0上任一点P,过引圆的切线PQ(Q为切点),则|PQ|=
的圆心A(-2,-2),直线x-y+3=0上任一点P,过引圆的切线PQ(Q为切点),则|PQ|=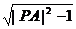 ,当且仅当|PA|最小时|PQ|最小,易见|PA|的最小值即A到直线x-y+3=0的距离,为
,当且仅当|PA|最小时|PQ|最小,易见|PA|的最小值即A到直线x-y+3=0的距离,为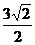 ,此时|PQ|=
,此时|PQ|=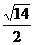 ,选B。
,选B。
[举例2] 能够使得圆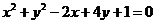 上恰有两个点到直线
上恰有两个点到直线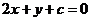 距离等于1的
距离等于1的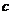 的一个值为:A.2 B.
的一个值为:A.2 B.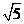 C.3
D.
C.3
D.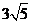
解析:本题如果设圆上一点的坐标,用点到直线的距离公式得到一个方程,进而研究方程解的个数,将是非常麻烦的。注意到圆心M(1,-2),半径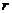 =2,结合图形容易知道,当且仅当M到直线
=2,结合图形容易知道,当且仅当M到直线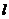 :
: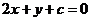 的距离
的距离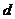 ∈(1,3)时,⊙M上恰有两个点到直线
∈(1,3)时,⊙M上恰有两个点到直线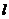 的距离等于1,由
的距离等于1,由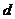 =
=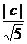 ∈(1,3)得:
∈(1,3)得: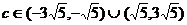 ,选C。
,选C。
[巩固1] 若直线(1+a)x+y+1=0与圆x2+y2-2x=0相切,则a的值为 ( )
(A)1,-1 (B)2,-2 (C)1 (D)-1
[巩固2]直线l1:y=kx+1与圆C:x2+y2+2kx+2my=0的两个交点A、B关于直线l2:x+y=0对称,则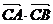 = 。
= 。
[迁移]实数x,y满足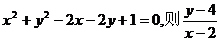 的取值范围为 ( )
的取值范围为 ( )
A.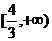 B.
B.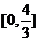 C.
C.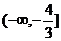 D.
D.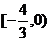
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com