
16.(本小题满分14分)
如图,已知AB⊥平面ACD,DE//AB,△ACD是正三角形,
AD=DE=2AB,且F是CD的中点。
(I)求证:AF//平面BCE;
(II)求证:平面BCE⊥平面CDE;
数学试卷 第2页(共4页)
15. (本小题满分14分)
△ABC中,角A的对边长等于2,向量m=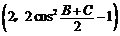 ,向量n=
,向量n=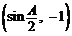 .
.
(1)求m·n取得最大值时的角A的大小;
(2)在(1)的条件下,求△ABC面积的最大值.

13. 若函数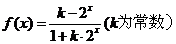 在定义域上为
在定义域上为 奇函数,则 k的值为 ▲ ..
奇函数,则 k的值为 ▲ ..
14 已知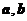 是两个互相垂直的单位向量, 且
是两个互相垂直的单位向量, 且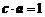 ,
,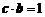 ,
,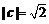 ,则对任意的正实
,则对任意的正实
数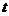 ,
,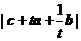 的最小值是
▲ .
的最小值是
▲ .
12.已知如下结论:“等边三角形内任意一点到各边的距离之和等于此三角形的高”,将此结论拓展到空间中的正四面体(棱长都相等的三棱锥),可得出的正确结论是:
▲ ▲ ▲
11.已知数列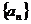 中,
中,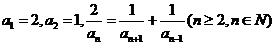 ,其通项公式
,其通项公式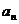 = ▲ .
= ▲ .
10.已知椭圆的中心在原点、焦点在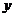 轴上,若其离心率是
轴上,若其离心率是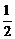 ,焦距是8,则该椭圆的方程为 ▲ .
,焦距是8,则该椭圆的方程为 ▲ .
9.函数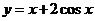 在区间
在区间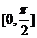 上的最大值是 ▲ .
上的最大值是 ▲ .
8. 已知实数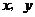 满足
满足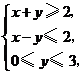 则
则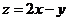 的取值范围是 ▲ .
的取值范围是 ▲ .
7. 在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出两个小球,则取出的小球上标注的数字之和为5或7的概率是 ▲ .
 数学试卷 第1页(共4页)
数学试卷 第1页(共4页)
6.已知直线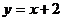 与曲线
与曲线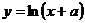 相切,则
相切,则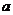 的值为
▲ .
的值为
▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com