
21、(本小题满分13分)设函数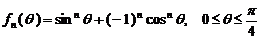 ,其中
,其中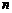 为正整数.
为正整数.
(Ⅰ)判断函数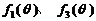 的单调性,并就
的单调性,并就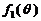 的情形证明你的结论;
的情形证明你的结论;
(Ⅱ)证明: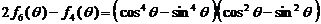 ;
;
(Ⅲ)对于任意给定的正整数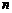 ,求函数
,求函数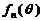 的最大值和最小值.
的最大值和最小值.
20、(本小题满分13分)椭圆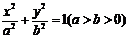 的左、右焦点分别为F1、F2,过F1的直线l与椭圆交
的左、右焦点分别为F1、F2,过F1的直线l与椭圆交
于A、B两点.
(Ⅰ)如果点A在圆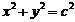 (c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;
(c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;
(Ⅱ)若函数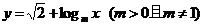 的图象,无论m为何值时恒过定点(b,a),
的图象,无论m为何值时恒过定点(b,a),
求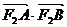 的取值范围.
的取值范围.
19、(本小题满分13分)已知数列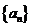 满足
满足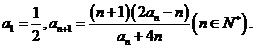
(Ⅰ)求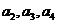 ;
;
(Ⅱ)已知存在实数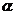 ,使
,使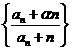 为公差为
为公差为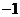 的等差数列,求
的等差数列,求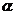 的值;
的值;
(Ⅲ)记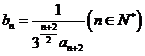 ,数列
,数列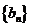 的前
的前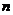 项和为
项和为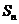 ,求证:
,求证: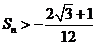 .
.
18、 (本小题满分12分)如图,斜三棱柱
(本小题满分12分)如图,斜三棱柱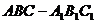 ,已知侧面
,已知侧面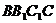 与底面ABC垂直且∠BCA =90°,∠
与底面ABC垂直且∠BCA =90°,∠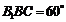 ,
,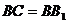 =2,若二面角
=2,若二面角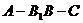 为30°.
为30°.
(Ⅰ)证明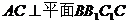 ;
;
(Ⅱ)求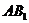 与平面
与平面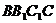 所成角的正切值;
所成角的正切值;
(Ⅲ)在平面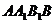 内找一点P,使三棱锥
内找一点P,使三棱锥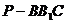 为正三棱锥,
为正三棱锥,
并求P到平面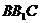 距离.
距离.
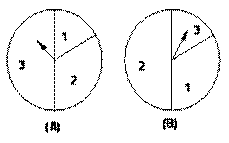 16、(本小题满分10分)如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为
16、(本小题满分10分)如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为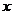 ,转盘(B)指针所对的区域为
,转盘(B)指针所对的区域为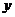 ,
,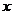 、
、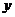
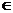
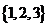 ,设
,设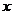 +
+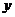 的值为
的值为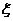 ,每一次游戏得到奖励分为
,每一次游戏得到奖励分为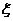 .
.
(Ⅰ)求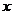 <2且
<2且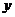 >1的概率;
>1的概率;
(Ⅱ)某人进行了12次游戏,求他平均可以得到的奖励分.
17、(本小题满分12分)在△OAB的边OA、OB上分别有一点P、Q,已知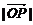 :
: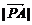 =1:2,
=1:2, 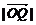 :
: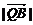 =3:2,连结AQ、BP,设它们交于点R,若
=3:2,连结AQ、BP,设它们交于点R,若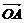 =a,
=a,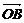 =b.
=b.
(Ⅰ)用a与 b表示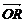 ;
;
(Ⅱ)过R作RH⊥AB,垂足为H,若| a|=1, | b|=2, a与 b的夹角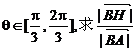 的范围.
的范围.
15、函数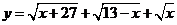 的最小值为
,最大值为
.
的最小值为
,最大值为
.
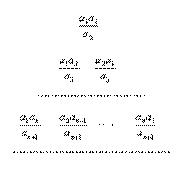
14、已知数列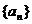 满足:
满足: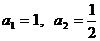 ,且
,且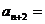
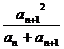 (
(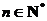 ),
),
则右图中前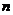 行所有数的和
行所有数的和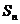 = .
= .
13、若方程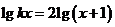 仅有一个实根,那么
仅有一个实根,那么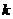 的取值范围是 .
的取值范围是 .
11、已知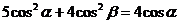 ,则
,则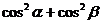 的取值范围是_______________.
的取值范围是_______________.
 12、甲、乙两厂生产同一种商品.甲厂生产的此商品占市场上的80%,乙厂生产的占20%;甲厂商品的合格率为95%,乙厂商品的合格率为90%.若某人购买了此商品发现为次品,则此次品为甲厂生产的概率为 .
12、甲、乙两厂生产同一种商品.甲厂生产的此商品占市场上的80%,乙厂生产的占20%;甲厂商品的合格率为95%,乙厂商品的合格率为90%.若某人购买了此商品发现为次品,则此次品为甲厂生产的概率为 .
10、数列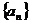 的各项均为正数,
的各项均为正数,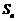 为其前
为其前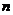 项和,对于任意
项和,对于任意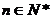 ,总有
,总有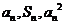 成等差数列设数列
成等差数列设数列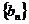
的前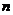 项和为
项和为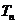 ,且
,且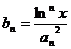 ,则对任意实数
,则对任意实数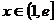 (
(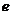 是常数,
是常数,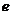 =2.71828
=2.71828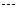 )和任意正整数
)和任意正整数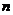 ,
,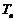 小于的最小正整数为 ( )
小于的最小正整数为 ( )
A、1 B、2 C、3 D、4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com