
16. 已知数列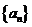 的前n项和
的前n项和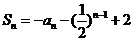 (n为正整数)。
(n为正整数)。
(Ⅰ)令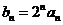 ,求证数列
,求证数列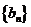 是等差数列,并求数列
是等差数列,并求数列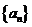 的通项公式;
的通项公式;
(Ⅱ)令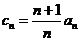 ,
,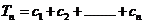 试比较
试比较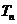 与
与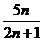 的大小,并予以证明。
的大小,并予以证明。
15. 已知数集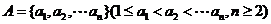 具有性质
具有性质 ;对任意的
;对任意的
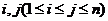 ,
,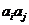 与
与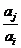 两数中至少有一个属于
两数中至少有一个属于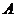 。
。
(I)分别判断数集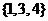 与
与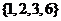 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(Ⅱ)证明: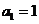 ,且
,且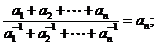
(Ⅲ)证明:当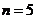 时,
时,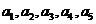 成等比数列。
成等比数列。
14. 已知等差数列有一性质:若等差数列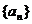 ,则通项为
,则通项为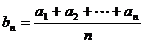 的数列
的数列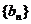 也是等差数列。类比上述命题,相应的等比数列有性质:若
也是等差数列。类比上述命题,相应的等比数列有性质:若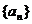 是等比数列
是等比数列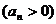 ,则通项为
,则通项为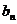 =
的数列也是等比数列
=
的数列也是等比数列
13. 已知数列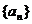 的前n项和
的前n项和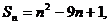 则其通项an=
;若它的第k项满足
则其通项an=
;若它的第k项满足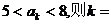 .
.
12. 数列1,2,2,3,3,3,4,4,4,4,5……的第100项是
11. 在数列中,已知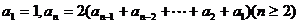 ,这个数列的通项公式是
,这个数列的通项公式是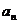 =
。
=
。
10. 已知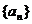 为等差数列,
为等差数列,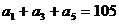 ,
, ,以
,以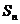 表示
表示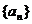 的前
的前 项和,则使得
项和,则使得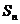 达到最大值的
达到最大值的 是
是
A.21 B.20 C.19 D.18
9. 等比数列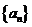 的前n项和为
的前n项和为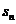 ,且4
,且4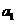 ,2
,2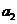 ,
,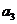 成等差数列。若
成等差数列。若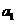 =1,则
=1,则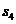 =
=
A.7 B.8 C.15 D.16
8. 数列{ 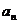 } 的通项
} 的通项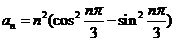 ,其前n项和为
,其前n项和为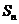 ,则
,则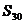 为
为
A.470 B.490 C.495 D.510
7. 设等比数列{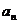 }的前n 项和为
}的前n 项和为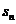 ,若
,若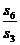 =3 ,则
=3 ,则 =
=
A.2 B.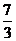 C.
C.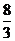 D.3
D.3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com