
4.已知点P(x,y)在不等式表示的平面区域上运动,则z=x-y的取值范围是
A.[-2,-1] B.[-2,1] C.[-1,2] D.[1,2]
3.设方程2x+x+2=0和方程log2x+x+2=0的根分别为p和q,函数f(x)=(x+p)(x+q)+2,则
A.f(2)=f(0)<f(3) B.f(0)<f(2)<f(3) C.f(3)<f(0)=f(2) D.f(0)<f(3)<f(2)
2.如图,直线Ax+By+C=0(AB≠0)的右下方有一点(m,n),则Am+Bn+C的值
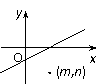 A.与A同号,与B同号
A.与A同号,与B同号
B.与A同号,与B异号
C.与A异号,与B同号
D.与A异号,与B异号
只有一项是符合题目要求的.
1.设全集U=R,集合A=(1,+∞),集合B=(-∞,2)。则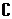 U(A∩B)=
U(A∩B)=
A.(-∞,1)∪(2,+∞) B.(-∞,1)∪[2,+∞)
C.(-∞,1]∪[2,+∞) D.(-∞,1]∪(2,+∞)
16. 解:(I)在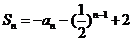 中,令n=1,可得
中,令n=1,可得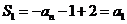 ,即
,即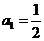
当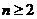 时,
时,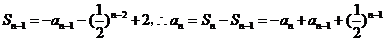 ,
,

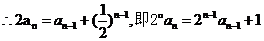 .
.
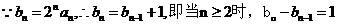 .
.
又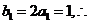 数列
数列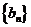 是首项和公差均为1的等差数列.
是首项和公差均为1的等差数列.
于是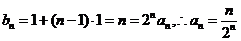 .
.
(II)由(I)得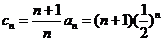 ,所以
,所以
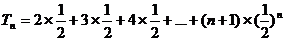 ①
①
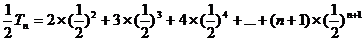 ②
②
由①-②得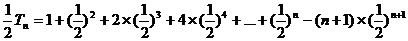
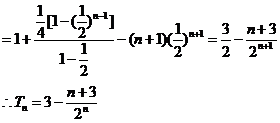
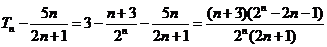
于是确定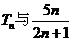 的大小关系等价于比较
的大小关系等价于比较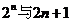 的大小
的大小
由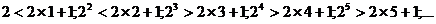
可猜想当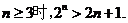 证明如下:
证明如下:
证法1:(1)当n=3时,由上验算显示成立。
(2)假设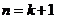 时
时
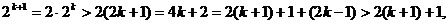
所以当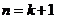 时猜想也成立
时猜想也成立
综合(1)(2)可知 ,对一切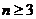 的正整数,都有
的正整数,都有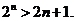
证法2:当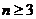 时
时
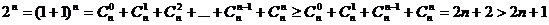
综上所述,当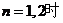
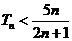 ,当
,当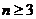 时
时
15. 解:本题主要考查集合、等比数列的性质,考查运算能力、推理论证能力、
分类讨论等数学思想方法.本题是数列与不等式的综合题,属于较难层次题.
(Ⅰ)解:由于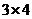 与
与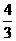 均不属于数集
均不属于数集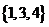 ,∴该数集不具有性质P.
,∴该数集不具有性质P.
由于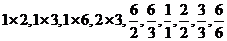 都属于数集
都属于数集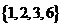 ,
,
∴该数集具有性质P.
(Ⅱ)证明:∵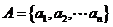 具有性质P,∴
具有性质P,∴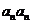 与
与 中至少有一个属于A,
中至少有一个属于A,
由于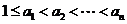 ,∴
,∴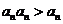 ,故
,故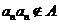 .
.
从而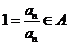 ,∴
,∴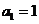 .
.
∵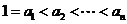 , ∴
, ∴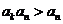 ,故
,故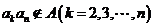 .
.
由A具有性质P可知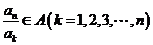 .
.
又∵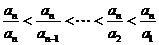 ,∴
,∴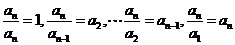 ,
,
从而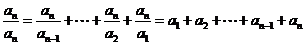 ,
,
∴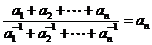 .
.
(Ⅲ)由(Ⅱ)知,当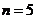 时,有
时,有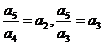 ,即
,即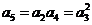 ,
,
∵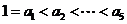 ,∴
,∴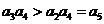 ,∴
,∴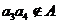 ,
,
由A具有性质P可知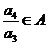 .
.
由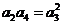 ,得
,得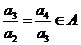 ,且
,且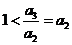 ,∴
,∴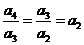 ,
,
∴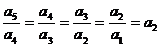 ,即
,即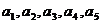 是首项为1,公比为
是首项为1,公比为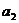 成等比数列。
成等比数列。
14. 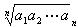
13. 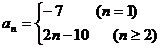 ,8
,8
12. 14
11. 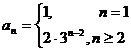
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com