
5. 命题 “存在实数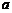 ,
,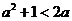 ”的否定为 ▲ 命题.(填“真”或“假”)
”的否定为 ▲ 命题.(填“真”或“假”)
4.函数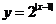 的值域为 ▲ .
的值域为 ▲ .
3.方程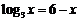 的根在区间
的根在区间 ,则整数
,则整数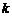 的值为 ▲ .
的值为 ▲ .
2.设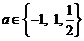 ,则使函数
,则使函数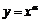 的定义域为
的定义域为 且为奇函数的所有
且为奇函数的所有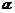 值为 ▲ .
值为 ▲ .
1.已知集合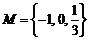 ,
,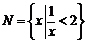 ,则
,则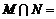 ▲ .
▲ .
20.(本题满分16分)已知函数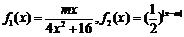 ,其中
,其中 .
.
(1)若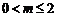 ,试求函数
,试求函数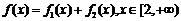 的最小值;
的最小值;
(2)设函数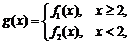 若对于任意大于等于2的实数
若对于任意大于等于2的实数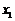 ,总存在唯一的小于2的实数
,总存在唯一的小于2的实数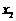 ,使得
,使得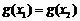 成立,试确定实数
成立,试确定实数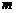 的取值范围.
的取值范围.
19.(本题满分16分)某污水处理厂要在一个矩形处理池(如图所示的四边形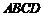 )的池底水平铺设污水净化管道(构成三角形
)的池底水平铺设污水净化管道(构成三角形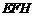 )处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口
)处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口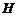 是
是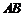 的中点,
的中点,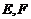 分别落在线段
分别落在线段 上,且
上,且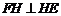 .已知
.已知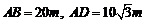 ,记
,记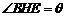 .
.
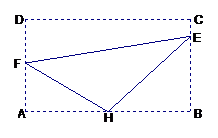 (1)试将污水净化管道的长度
(1)试将污水净化管道的长度 表示为
表示为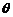 的函数,并写出定义域;
的函数,并写出定义域;
(2)问:当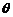 取何值时,铺设管道的成本最低?并求出此时管道的长度.
取何值时,铺设管道的成本最低?并求出此时管道的长度.
18.(本题满分15分)已知数列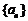 是等差数列,
是等差数列, 是等比数列,
是等比数列,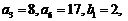
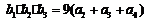 .
.
(1)分别求数列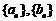 的通项公式;
的通项公式;
(2)设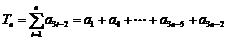 ,求
,求 ;
;
(3)求满足不等式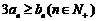 成立的
成立的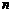 的值.
的值.
17.(本题满分15分)已知函数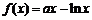 ,
,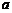 为常数且
为常数且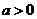 .
.
(1)如果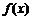 在
在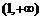 上单调递增,求实数
上单调递增,求实数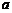 的取值范围;
的取值范围;
(2)求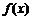 在
在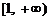 上的最小值.
上的最小值.
16.(本题满分14分)已知在 中,
中,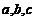 分别为角
分别为角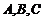 所对的边,
所对的边, .
.
(1)求角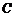 的大小;
的大小;
(2)若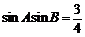 ,试判断
,试判断 的形状,并说明理由.
的形状,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com