
15.(本题满分15分)某商场在促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费一定金额后,按以下方案获得相应金额的奖券:
|
消费金额(元)的范围 |
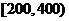 |
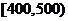 |
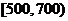 |
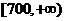 |
|
获得奖券的金额(元) |
30 |
60 |
100 |
120 |
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如:购买标价为400元的商品,则消费金额为320元,获得的优惠额为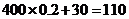 (元).设购买商品得到的优惠率=
(元).设购买商品得到的优惠率= ,试问:
,试问:
(1)购买一件标价为1200元的商品,顾客得到的优惠率是多少?
(2)对于标价在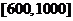 元内的商品,顾客购买商品标价在什么范围内时,可得到不小于
元内的商品,顾客购买商品标价在什么范围内时,可得到不小于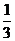 的优惠率?
的优惠率?
14.(本题满分14分)某班从8名学生干部中(其中男生4人,女生4人),选3人参加学校的义务劳动.
(1)设所选3人中女生人数ξ,求ξ的分布列及数学期望;
(2)求男生甲或女生乙被选中的概率.
13.(本题满分14分)已知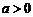 ,设命题
,设命题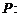 函数
函数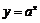 在
在 上单调递增;命题
上单调递增;命题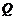 :不等式
:不等式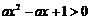 对
对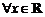 恒成立,若
恒成立,若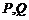 中有且只有一个为真,求
中有且只有一个为真,求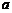 的取值范围.
的取值范围.
12.(本题满分10分)已知曲线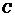 的极坐标方程是
的极坐标方程是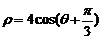 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为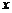 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线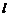 的参数方程是:
的参数方程是: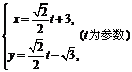 ,求直线
,求直线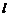 与曲线
与曲线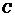 相交弦的弦长.
相交弦的弦长.
11.(本题满分10分)已知矩阵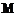
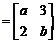 ,其中
,其中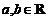 ,若点
,若点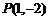 在矩阵
在矩阵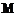 的变换下得到点
的变换下得到点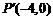 ,求实数
,求实数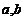 的值.
的值.
10.已知函数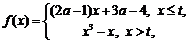 ,无论t取何值,函数f(x)在区间(-∞,+∞)总是不单调.则a的取值范围是 ▲ .
,无论t取何值,函数f(x)在区间(-∞,+∞)总是不单调.则a的取值范围是 ▲ .
9.定义:区间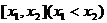 的长度为
的长度为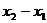 .已知函数
.已知函数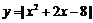 定义域为
定义域为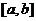 ,值域为
,值域为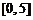 ,则区间
,则区间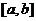 的长度的最大值为 ▲ .
的长度的最大值为 ▲ .
8.若“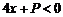 ”是“
”是“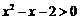 ”的充分不必要条件,则实数
”的充分不必要条件,则实数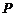 的取值范围是 ▲ .
的取值范围是 ▲ .
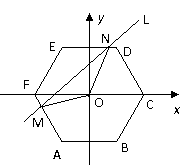
7.如图,在直角坐标平面内有一个边长为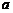 、中心在原点
、中心在原点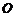 的
的
正六边形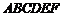 ,
,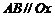 .
直线
.
直线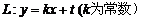 与正六边形交于
与正六边形交于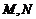 两点,记
两点,记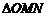 的面积为
的面积为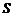 ,则函数
,则函数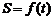 的奇偶性为 ▲ (填“奇函数”或“偶函数”或“非奇非偶函数”之一) .
的奇偶性为 ▲ (填“奇函数”或“偶函数”或“非奇非偶函数”之一) .
6.直线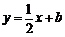 能作为下列函数
能作为下列函数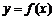 的切线有 ▲ .
的切线有 ▲ .
 ①
①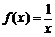 ②
②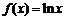 ③
③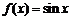 ④
④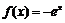
(写出所有正确的函数序号) .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com