
6、王国维之死
王国维的文化生命中,最深奥的一笔是他的死。
关于他的死,赵万里《王静安先生年谱》有如下记载:“五月初二日夜,阅试卷毕,草遗书怀之。是夜熟眠如常。翌晨(即1927年6月2日)盥洗饮食,赴研究院视事亦如常。忽于友人处假银饼五枚,独行出校门,雇车至颐和园。步行至排云轩西鱼藻轩前,临流独立,尽纸烟一支,园丁曾见之,忽闻有落水声,争往援起,不及二分钟已气绝矣,时正巳正也。”
由此大体可以推测,王国维的死,不仅是一种主动的选择,而且平静得很,如同去赴一位老朋友的约会,没有丝毫激昂的成分。正是这种视死如归的平静,为王国维在文化史的坐标系上圈定了一个独特的位置。他并非死于具体的时事,而极可能是死于对他身处其中的文化精神的失望,对于中国文化中某些无法补救的缺失的绝望。从大的历史观来看,他的死,不仅不拘泥于一些具体时务,更超越了个体生命;他以死来将自己同沦落的文化分割开来--他看到,倘肉体不死,精神必定走向泯灭,所以,只有以肉体的死,换取精神的永生。这正是他的大清醒、大智慧处。当时恐怕只有少数有同感者看穿了这一点。
分析:宁静无悔的选择,似乎在追求着什么,也许是中国知识分子那内心深处的一种恬然吧!
话题:“选择和追求”“死亡与永生”
5、炙肘练笔
当代画家潘觐缋于上海艺专毕业后,回到家乡卖画为生。他在恶劣的环境下刻苦练画,常十几个小时不停地练。晚上他就在煤油灯下练画,还找到了治瞌睡的最好办法。每当夜间作画困意缠绕,难以自制时,他就把臂膀伸到灯罩上,滚烫的煤油灯玻璃罩发出“嗤”的一声。剧痛驱散了他的睡意,又提起精神继续作画。久而久之,他的左膀肘上留下几块黑色瘢痕。他刻苦学画作画,终获成功。他的鱼类画,风格特异,独树一帜,蜚声中外。
分析:学习既要讲究方法,也需要毅力。任何想投机取巧的人都不可能获得成功。
话题:“刻苦”“成功的法则”
4、不达目的不罢休
语言大师侯宝林只上过三年小学,由于勤奋好学,他的艺术水平达到炉火纯青的程度,成为著名的语言专家。有一次,他为了买到自己想买的一部明代笑话书《谑浪》,跑遍北京所有的旧书摊也未如愿。后来,他得知北京图书馆有这本书。时值冬日,他顶着狂风,冒着大雪,一连18天都跑到图书馆去抄书,一部10万字的书,终于被他抄录到手。侯宝林正是凭着“不达目的不罢休”的坚强毅力,才成为一代相声艺术宗师的。
分析:语言大师侯宝林以他的行动告诉我们这样的道理:要想成就一番事业,一要勤奋好学,二要持之以恒。
话题:“笑声来自勤奋”“学习成就天才”
3、李宁带伤比赛夺金牌
在奥运会上连夺3块金牌的李宁是带伤参加比赛的。1984年5月,严重的伤痛使他放弃了在南昌举行的全国体操赛。奥运会临近,伤痛稍有好转,他就参加训练,去洛杉矶后,有一天做双杠后滚翻直倒立拉臂时,一使劲,胸肌拉伤了,肩背也受伤,痛得他痉挛抽搐,攥紧拳头。可他瞒着教练,暗暗发誓:“拼吧,就是比赛后肩膀断了,我也认了!”就这样,李宁不仅靠他的体力、技术,还靠他的坚强意志夺得了3块金牌。
分析:金牌是重要的,比金牌更重要的是精神。体育场上最感动人们的,就是这种拼搏精神。
话题:“最重的金牌”“精神无价”
2、童第周新婚别爱妻
1930年,童第周刚结婚,为了深造,他毅然告别了妻子,到比利时留学。他们坚信:“两情若是长久时,又岂在朝朝暮暮!”这一去,就是4年。妻子在家养育着孩子,还把菲薄的工资省下一些寄给国外几乎一贫如洗的童第周,他不禁热泪盈眶。4年后童回国,二人从此并肩在实验室探索着生物学的奥秘。
分析:求知者,有时近于无情者;看似无情,却是至情。
话题:“有情与无情”“追求”
1、金兵未灭,何以为家
北宋末年的民族英雄岳飞,在金人入侵的动乱年代里,立下了“还我河山”的壮志,他一生征战沙场,死而后已。当岳飞率领军队屡败金兵,建有大功的时候,有人赠送美女以示慰劳,岳飞说:“金兵未灭,难道是大将安乐的时候吗?”宋高宗要为他建宅第、立家室,以褒奖他的赫赫战功,他又辞谢道:“金兵未灭,何以为家?”岳飞一生矢志不渝,终于留下千古美名。
分析:人生短暂,什么最重要?有的人选择及时行乐,有的人选择舒适安逸,岳飞选择的却是为了自己的理想和抱负,为了更多人的幸福而放弃小我。
话题:“生命的价值”“享乐与追求”
21.(13分)设数列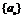 的首项
的首项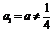 ,且
,且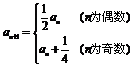 ,
,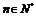 ,记
,记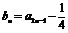 ,
, ,
,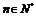 .
.
⑴求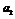 ,
,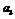 ;
;
⑵判断数列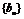 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
⑶当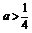 时,数列
时,数列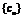 前
前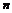 项和为
项和为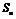 ,求
,求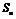 最值.
最值.




20.(13分)已知椭圆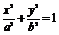
 ,
,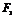 、
、 为其左右两焦点;两定点
为其左右两焦点;两定点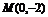 ,
,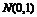 ,若椭圆上存在点
,若椭圆上存在点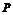 使
使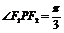 .
.
⑴求椭圆的离心率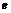 的取值范围;
的取值范围;
⑵若这样的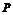 点有且只有2个,且
点有且只有2个,且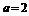 ,过点
,过点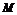 的直线
的直线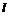 与椭圆相交于
与椭圆相交于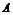 、
、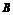 两点,线段
两点,线段 的中点为
的中点为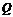 ,直线
,直线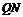 与
与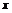 轴交点横坐标为
轴交点横坐标为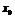 ,求
,求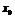 的取值范围.
的取值范围.
19.(13分)已知函数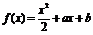 ,其中
,其中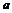 、
、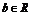 ,
,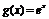 (
(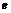 是自然对数的底).
是自然对数的底).
⑴当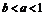 ,
,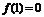 ,且函数
,且函数 的零点,证明:
的零点,证明: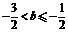 ;
;
⑵当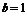 时,若不等式
时,若不等式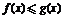 在
在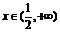 恒成立,求
恒成立,求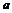 的取值范围.
的取值范围.
18.(12分)如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),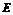 为
为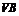 的中点.
的中点.
⑴求证: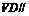 平面
平面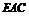 ;⑵求二面角
;⑵求二面角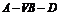 的正切值.
的正切值.
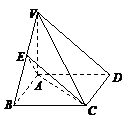

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com