
4.把函数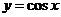 图象沿
图象沿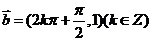 平移,得到函数 的图象.
平移,得到函数 的图象.
3.已知一个平行四边形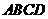 的顶点
的顶点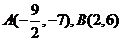 ,对角线的交点为
,对角线的交点为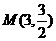 ,则它的另外两个顶点的坐标为
.
,则它的另外两个顶点的坐标为
.
2.下列条件中,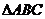 是锐角三角形的是 ( )
是锐角三角形的是 ( )
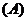
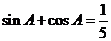
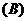
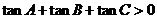
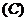
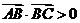
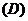
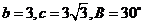
1.正方形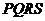 对角线交点为
对角线交点为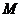 ,坐标原点
,坐标原点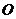 不在正方形内部,且
不在正方形内部,且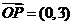 ,
,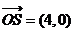 ,则
,则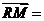 ( )
( )
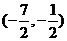
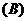
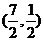
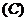
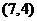
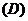
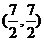
2.渗透数学建模的思想,切实培养分析和解决问题的能力.
1.进一步熟练有关向量的运算和证明;能运用解三角形的知识解决有关应用问题,
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.若函数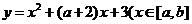 的图象关于
的图象关于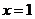 对称则
对称则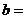 6 .
6 .
2.二次函数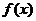 的二次项系数为负值,且
的二次项系数为负值,且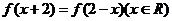 ,问
,问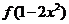 与
与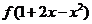 满足什么关系时,有
满足什么关系时,有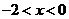 .
.
3.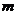 取何值时,方程
取何值时,方程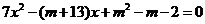 的一根大于
的一根大于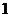 ,一根小于
,一根小于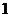 .
.
(三)例题分析:
例1.函数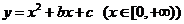 是单调函数的充要条件是 (
是单调函数的充要条件是 ( 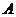 )
)
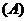
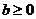
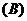
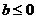
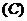
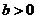
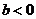
分析:对称轴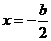 ,∵函数
,∵函数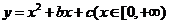 是单调函数,
是单调函数,
∴对称轴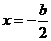 在区间
在区间
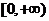 的左边,即
的左边,即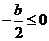 ,得
,得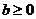 .
.
例2.已知二次函数的对称轴为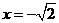 ,截
,截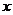 轴上的弦长为
轴上的弦长为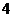 ,且过点
,且过点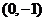 ,求函数的解析式.
,求函数的解析式.
解:∵二次函数的对称轴为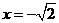 ,设所求函数为
,设所求函数为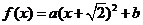 ,又∵
,又∵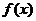 截
截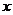 轴上的弦长为
轴上的弦长为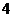 ,∴
,∴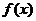 过点
过点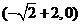 ,
,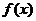 又过点
又过点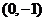 ,
,
∴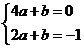 ,
, 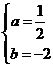 ,
,
∴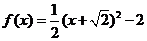 .
.
例3.已知函数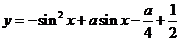 的最大值为
的最大值为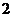 ,求
,求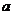 的值 .
的值 .
分析:令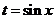 ,问题就转二次函数的区间最值问题.
,问题就转二次函数的区间最值问题.
解:令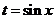 ,
,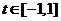 ,
,
∴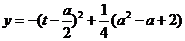 ,对称轴为
,对称轴为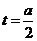 ,
,
(1)当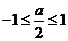 ,即
,即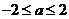 时,
时,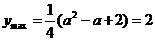 ,得
,得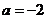 或
或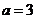 (舍去).
(舍去).
(2)当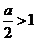 ,即
,即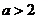 时,函数
时,函数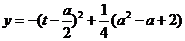 在
在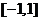 单调递增,
单调递增,
由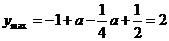 ,得
,得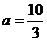 .
.
(3)当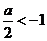 ,即
,即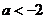 时,函数
时,函数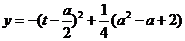 在
在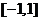 单调递减,
单调递减,
由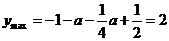 ,得
,得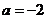 (舍去).
(舍去).
综上可得: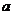 的值为
的值为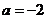 或
或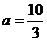 .
.
例4. 已知函数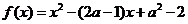 与非负
与非负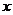 轴至少有一个交点,求
轴至少有一个交点,求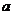 的取值范围.
的取值范围.
解法一:由题知关于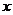 的方程
的方程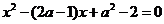 至少有一个非负实根,设根为
至少有一个非负实根,设根为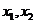
则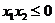 或
或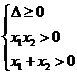 ,得
,得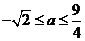 .
.
解法二:由题知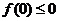 或
或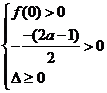 ,得
,得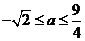 .
.
例5.对于函数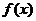 ,若存在
,若存在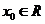 ,使
,使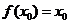 ,则称
,则称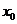 是
是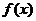 的一个不动点,已知函数
的一个不动点,已知函数
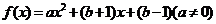 ,
,
(1)当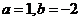 时,求函数
时,求函数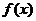 的不动点;
的不动点;
(2)对任意实数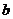 ,函数
,函数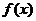 恒有两个相异的不动点,求
恒有两个相异的不动点,求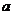 的取值范围;
的取值范围;
(3)在(2)的条件下,若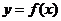 的图象上
的图象上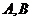 两点的横坐标是
两点的横坐标是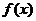 的不动点,且
的不动点,且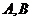 两点关于直线
两点关于直线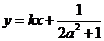 对称,求
对称,求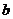 的最小值.
的最小值.
解:(1)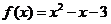 ,
,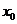 是
是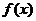 的不动点,则
的不动点,则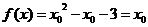 ,得
,得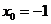 或
或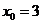 ,函数
,函数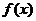 的不动点为
的不动点为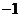 和
和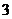 .
.
(2)∵函数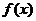 恒有两个相异的不动点,∴
恒有两个相异的不动点,∴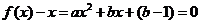 恒有两个不等的实根,
恒有两个不等的实根,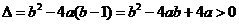 对
对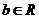 恒成立,
恒成立,
∴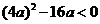 ,得
,得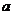 的取值范围为
的取值范围为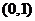 .
.
(3)由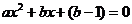 得
得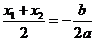 ,由题知
,由题知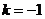 ,
,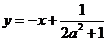 ,
,
设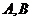 中点为
中点为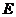 ,则
,则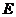 的横坐标为
的横坐标为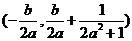 ,∴
,∴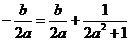 ,
,
∴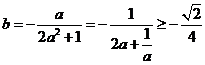 ,当且仅当
,当且仅当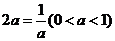 ,即
,即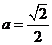 时等号成立,
时等号成立,
∴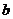 的最小值为
的最小值为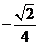 .
.
(二)主要方法:
1.讨论二次函数的区间最值问题:①注意对称轴与区间的相对位置;②函数在此区间上的单调性;
2.讨论二次函数的区间根的分布情况一般需从三方面考虑:①判别式;②区间端点的函数值的符号;③对称轴与区间的相对位置.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com