
5. -Mum, would you buy some cherries for me? I love them.
-I’d like to, but they are not ________ in winter.
|
A. accustomed |
B. convenient |
C. casual |
D. available |
4. Joanna won’t leave her job undone ________ told to.
|
A. when |
B. until |
C. unless |
D. as |
3. In the Spring Festival, Jonny sent each of his classmates a card with best wishes, but he received ________.
|
A. no one |
B. nothing |
C. some |
D. none |
2. -I’d like to buy ________ book recommended by our English teacher.
-But I don’t think it ________ good one.
|
A. a; the |
B. a; a |
C. the; a |
D. the; the |
第一节:单项选择(共20小题,每小题0.5分,满分10分)
1. - Good-bye ! I’m going back to my hometown this afternoon.
-________
|
A. Have a nice trip. |
B. Congratulations! |
|
C. Take your time. |
D. I couldn’t agree more. |
1.①内容:与文章的叙述内容紧密结合,(1分)含蓄地表达了作者对鸦片战争的深度思考。(1分)
②结构:三段诗句采用重章叠句的手法,贯穿始终,使文章脉络清楚,首尾呼应,一气呵成;在叙述中穿插,使行文多姿。(手法1分,作用任答一点1分)
③语言:诗段采用反复、拟人等手法,把浪花、海浪当作人来写(赋予浪花、海浪人的动作、思想),更含蓄、生动形象,更具表现力。(任答一种手法1分,分析作用1分)
1.请分别从内容、结构和语言三方面分析本文使用的三节诗句的作用。(6分)
(18)(本题满分14分)已知函数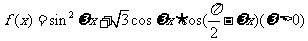 ,且函数
,且函数 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为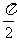 .
.
(Ⅰ)求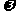 的值及
的值及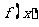 的单调递增区间;
的单调递增区间;
(Ⅱ)在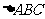 中,
中,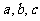 分别是角
分别是角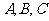 的对边,若
的对边,若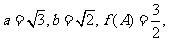 求角
求角
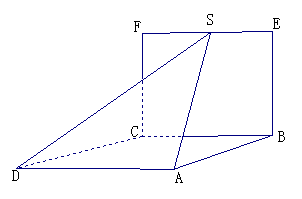 (19)(本题满分14分)已知
(19)(本题满分14分)已知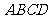 为平行四边形,
为平行四边形,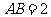 ,
,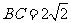 ,
,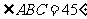 ,
,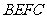 是长方形,
是长方形,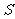 是
是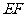 的中点,
的中点,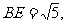 平面
平面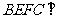 平面
平面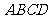 ,
,
(Ⅰ)求证: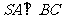 ;
;
(Ⅱ)求直线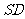 与平面
与平面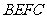 所
所
成角的正切值.
|
(20)(本题满分14分)对于给定数列 ,如果存在实常数
,如果存在实常数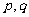 ,使得
,使得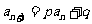 对于任意
对于任意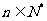 都成立,我们称数列
都成立,我们称数列 是 “
是 “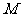 类数列”.
类数列”.
(Ⅰ)已知数列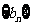 是 “
是 “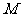 类数列”且
类数列”且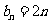 ,求它对应的实常数
,求它对应的实常数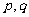 的值;
的值;
(Ⅱ)若数列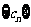 满足
满足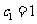 ,
,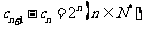 ,求数列
,求数列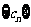 的通项公式.并判断
的通项公式.并判断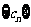 是否为“
是否为“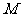 类数列”,说明理由.
类数列”,说明理由.
(21)(本题满分15分)已知函数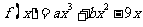 在
在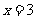 处取得极大值
处取得极大值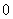 .
.
(Ⅰ)求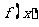 在区间
在区间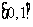 上的最大值;
上的最大值;
 (Ⅱ)若过点
(Ⅱ)若过点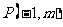 可作曲线
可作曲线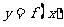 的切线有三条,求实数
的切线有三条,求实数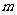 的取值范围.
的取值范围.
(22)(本题满分15分)已知抛物线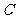 的方程
的方程
为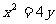 ,直线
,直线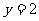 与抛物线
与抛物线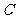 相交
相交
于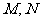 两点,点
两点,点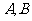 在抛物线
在抛物线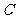 上.
上.
(Ⅰ)若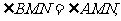 求证:直线
求证:直线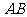
的斜率为定值;
(Ⅱ)若直线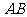 的斜率为
的斜率为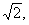 且点
且点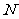 到
到
直线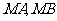 的距离的和为
的距离的和为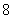 ,试判断
,试判断 的形状,并证明你的结论.
的形状,并证明你的结论.
台州市2010年高三年级第二次调考试题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com