
2.已知0<α<<β<π,cosα=,sin(α+β)=-,则cosβ的值为________.
解析:∵0<α<,<β<π,∴<α+β<π.∴sinα=,cos(α+β)=-,
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=(-)×+(-)×=-.答案:-
1.已知sinα=,sin(α-β)=-,α、β均为锐角,则β等于________.
解析:∵α、β均为锐角,∴-<α-β<,∴cos(α-β)==.
∵sinα=,∴cosα= =.
∴sinβ=sin[α-(α-β)]=sinαcos(α-β)-cosαsin(α-β)=.
∵0<β<,∴β=.答案:
8.设双曲线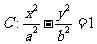
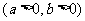 的离心率为
的离心率为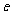 ,右准线
,右准线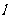 与两条渐近线交于
与两条渐近线交于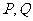 两点,右焦点为
两点,右焦点为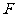 ,且
,且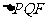 为等边三角形.
为等边三角形.
(1)求双曲线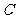 的离心率
的离心率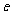 的值;(2)若双曲线
的值;(2)若双曲线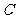 被直线
被直线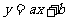 截得的弦长为
截得的弦长为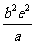 ,求双曲线
,求双曲线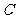 的方程;(3)设双曲线
的方程;(3)设双曲线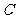 经过点
经过点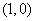 ,以
,以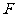 为左焦点,
为左焦点,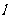 为左准线的椭圆,其短轴的端点为
为左准线的椭圆,其短轴的端点为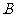 ,求
,求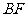 中点的轨迹方程.
中点的轨迹方程.
7.某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两个观测点晚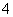
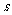 ,已知各观测点到中心的距离都是
,已知各观测点到中心的距离都是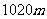 ,试确定该巨响发生的位置.(假定当时声音传播的速度为
,试确定该巨响发生的位置.(假定当时声音传播的速度为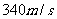 ;相关各点均在同一平面上)
;相关各点均在同一平面上)
6.如图, 7.设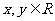
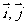 为直角坐标平面内
为直角坐标平面内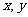 轴正方向上的单位向量,若向量
轴正方向上的单位向量,若向量
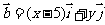 ,
,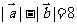 ,求点
,求点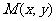 的轨迹C的方程.
的轨迹C的方程.
5.已知椭圆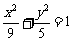 的两个焦点分别是F1、F2,△MF1F2的重心G恰为椭圆上的点,则点
的两个焦点分别是F1、F2,△MF1F2的重心G恰为椭圆上的点,则点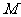 的轨迹方程为
.
的轨迹方程为
.
4.自椭圆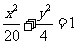 上的任意一点
上的任意一点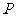 向
向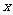 轴引垂线,垂足为
轴引垂线,垂足为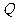 ,则线段
,则线段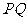 的中点
的中点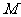 的轨迹方程为
的轨迹方程为
3.已知抛物线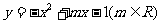 的顶点为
的顶点为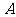 ,那么当
,那么当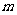 变化时,此抛物线焦点
变化时,此抛物线焦点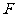 的轨迹方程是___________________________.
的轨迹方程是___________________________.
2.已知椭圆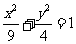 的左、右顶点分别为
的左、右顶点分别为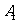 和
和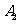 ,垂直于椭圆长轴的动直线与椭圆的两个交点分别为
,垂直于椭圆长轴的动直线与椭圆的两个交点分别为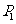 和
和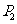 ,其中
,其中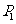 的纵坐标为正数,则直线
的纵坐标为正数,则直线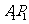 与
与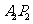 的交点
的交点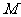 的轨迹方程
( )
的轨迹方程
( )
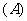

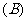
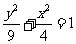
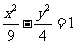
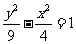
1.抛物线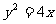 经过焦点的弦的中点的轨迹方程是
( )
经过焦点的弦的中点的轨迹方程是
( )
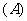
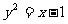
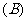
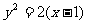
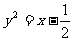
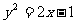
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com