
22.(本小题满分12分)设数列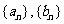 满足
满足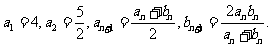
(1)用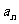 表示
表示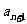 ,并证明:对任意正整数n ,都有
,并证明:对任意正整数n ,都有 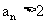 ;
;
(2)证明: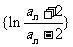 是等比数列;
是等比数列;
(3)设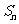 是数列
是数列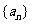 的前
的前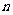 项和,当
项和,当 时,
时,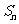 与
与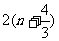 是否有确定的大小关系?若有,加以证明;若没有,请说明理由.
是否有确定的大小关系?若有,加以证明;若没有,请说明理由.
21.(本小题满分12分) 已知函数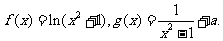
(1)求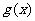 在
在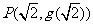 处的切线
处的切线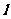 的方程;
的方程;
(2)若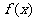 的一个极值点到直线
的一个极值点到直线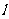 的距离为1,求
的距离为1,求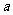 的值;
的值;
(3)求方程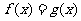 的根的个数.
的根的个数.
20.(本小题满分12分)一束光线从点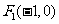 出发,经直线l:
出发,经直线l: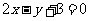 上一点
上一点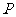 反射后,恰好穿过点
反射后,恰好穿过点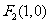 .
.
(1)求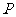 点的坐标;
点的坐标;
(2)求以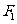 、
、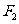 为焦点且过点
为焦点且过点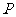 的椭圆
的椭圆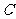 的方程;
的方程;
(3)设点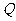 是椭圆
是椭圆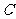 上除长轴两端点外的任意一点,试问在
上除长轴两端点外的任意一点,试问在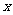 轴上是否存在两定点
轴上是否存在两定点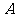 、
、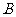 ,使得直线
,使得直线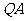 、
、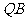 的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点
的斜率之积为定值?若存在,请求出定值,并求出所有满足条件的定点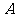 、
、 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
19.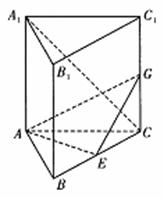 (本小题满分12分)如图,在直三棱柱ABC-A1B1C1中,
(本小题满分12分)如图,在直三棱柱ABC-A1B1C1中, E是BC的中点.
E是BC的中点.
(1)求异面直线AE与A1C所成的角;
(2)若G为C1C上一点,且EG⊥A1C,试确定点G的位置;
(3)在(2)的条件下,求二面角A1-AG-E的大小.
18.(本小题满分12分)全球金融危机,波及中国股市,甲、乙、丙、丁四人打算趁目前股市低迷之际“抄底”,若四人商定在圈定的6只股票中各自随机购买一只(假定购买时每支股票的基本情况完全相同).
(1)求甲、乙、丙、丁四人恰好买到同一只股票的概率;
(2)求甲、乙、丙、丁四人中至多有两人买到同一只股票的概率;
(3)由于中国政府采取了积极的应对措施,股市渐趋“回暖”.若某人今天按上一交易日的收盘价20元/股,买入某只股票1000股,且预计今天收盘时,该只股票比上一交易日的收盘价上涨10%(涨停)的概率为0.6,持平的概率为0.2,否则将下跌10%(跌停),求此人今天获利的数学期望(不考虑佣金、印花税等交易费用).
17.(本小题满分10分) 在△ABC中,A、B、C的对边分别为a、b、c,且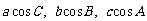 成等差数列.
成等差数列.
(1)求B的值;
(2)求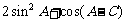 的范围.
的范围.
16.给出以下几个命题,正确的是
①函数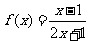 对称中心是
对称中心是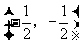 ;
;
②已知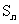 是等差数列
是等差数列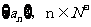 的前
的前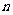 项和 ,若
项和 ,若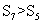 ,则
,则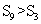 ;
;
③函数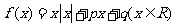 为奇函数的充要条件是
为奇函数的充要条件是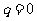 ;
;
④已知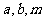 均是正数,且
均是正数,且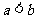 ,则
,则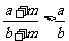 .
.
15.已知函数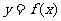 的反函数是
的反函数是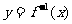 ,
,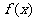 的图象在点
的图象在点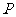 处的切线方程是
处的切线方程是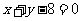 ,若点
,若点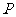 的横坐标是5,则
的横坐标是5,则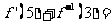 .
.
14.数列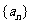 满足
满足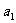 =1,
=1, 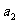 =
=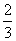 ,且
,且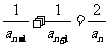 (n≥2),则
(n≥2),则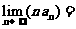 .
.
13.设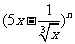 的展开式的各项系数之和为M,二项式系数之和为N,若M-N=240,则展开式中的常数项为_________.
的展开式的各项系数之和为M,二项式系数之和为N,若M-N=240,则展开式中的常数项为_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com