
5.袋中有6张卡片,编号分别是1.,2,3,4,5,6,现从袋中每次取一张卡片,取后放回,连续抽取三次,记三次中号码最大的数为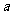 ,则概率
,则概率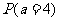 的值为
的值为
A. 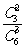 B.
B.
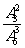 C.
C.
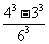 D.
D.
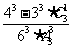
4.三棱锥P-ABC的高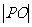 =
=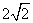 ,底面边长分别为3,4,5,Q点在底边上,且斜高PQ的数值为3,这样的Q点最多有
,底面边长分别为3,4,5,Q点在底边上,且斜高PQ的数值为3,这样的Q点最多有
A. 4个 B. 3个 C. 2个 D.1个
3.已知复数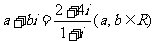 ,函数
,函数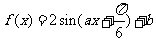 图象的一个对称中心是
图象的一个对称中心是
A.(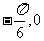 )
B. (
)
B. (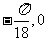 )
C.(
)
C.(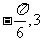 )
D.(
)
D.(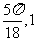 )
)
2.函数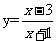
A. 在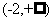 内单调递增 B. 在
内单调递增 B. 在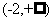 内单调递减
内单调递减
C. 在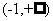 内单调递增 D. 在
内单调递增 D. 在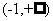 内单调递减
内单调递减
1.已知集合A, B,则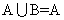 是
是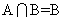 的
的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
22. 双曲线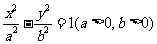 的离心率
的离心率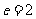 ,
,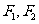 是左,右焦点,过
是左,右焦点,过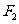 作
作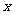 轴的垂线与双曲线在第一象限交于P点,直线F1P与右准线交于Q点,已知
轴的垂线与双曲线在第一象限交于P点,直线F1P与右准线交于Q点,已知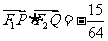
(1)求双曲线的方程;
(2)设过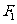 的直线MN分别与左支,右支交于M、N ,线段MN的垂线平分线
的直线MN分别与左支,右支交于M、N ,线段MN的垂线平分线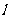 与
与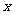 轴交于点
轴交于点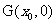 ,若
,若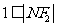 <3,求
<3,求 的取值范围。
的取值范围。
江西省重点中学协作体2010届高三第三次联考
21.(本题满分12分)已知函数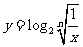
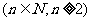
(1)当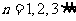 时,把已知函数的图像与直线
时,把已知函数的图像与直线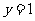 的交点的横坐标依次为
的交点的横坐标依次为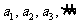 求证:
求证: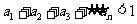
(2)对于每一个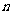 的值,设
的值,设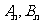 为已知函数的图上与
为已知函数的图上与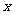 轴距离为1的两点,求证:
轴距离为1的两点,求证: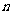 取任意一个正数时,以
取任意一个正数时,以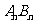 为直径的圆都与一条定直线相切,求这条定直线的方程和切点的坐标。
为直径的圆都与一条定直线相切,求这条定直线的方程和切点的坐标。
20.(本小题满分12分)
已知函数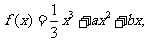 且
且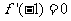
(1)求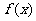 的单调区间;
的单调区间;
(2)令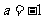 ,设函数
,设函数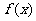 在
在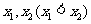 处取得极值,记点
处取得极值,记点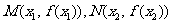 ,证明:线段
,证明:线段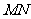 与曲线
与曲线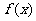 存在异于
存在异于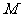 、
、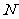 的公共点;
的公共点;
19.(本题满分12分)
(如图)已知四棱锥S-ABCD的底面ABCD是菱形,将面SAB,SAD,ABCD 展开成平面后的图形恰好为一正三角形 SC.
SC.
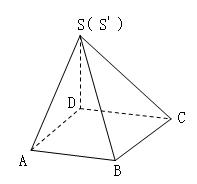
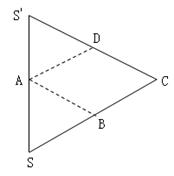
(1)求证:在四棱锥S-ABCD中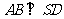 。
。
(2)若AC长等于6,求异面直线AB与SC之间的距离。
18.(本题满分12分)
中、日两国争夺某项国际博览会的申办权,进入最后一道程序,由国际展览局三名执委投票,决定承办权的最后归属。资料显示,A,B,C三名执委投票意向如下表所示
 |
中 国 |
日
本 |
|
A |
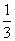 |
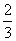 |
|
B |
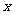 |
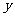 |
|
C |
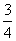 |
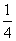 |
规定每位执委只有一票,且不能弃权,已知中国获得3票的概率为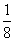 。
。
(1)求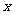 ,
,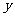 的值;
的值;
(2)求中国获得承办权的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com