
22.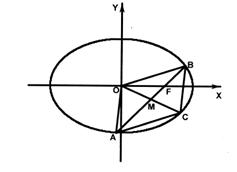 (本小题满分12分)已知椭圆
(本小题满分12分)已知椭圆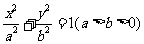 ,直线
,直线 与椭圆交于
与椭圆交于 、
、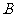 两点,
两点,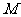 是线段
是线段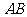 的中点,连接
的中点,连接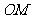 并延长交椭圆于点
并延长交椭圆于点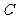 。
。
(Ⅰ)设直线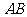 与直线
与直线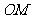 的斜率分别为
的斜率分别为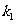 、
、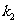 ,且
,且 ,求椭圆的离心率的取值范围。
,求椭圆的离心率的取值范围。
(Ⅱ)若直线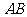 经过椭圆的右焦点
经过椭圆的右焦点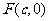 ,且四边形
,且四边形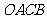 是面积为
是面积为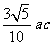 的平行四边形,求直线
的平行四边形,求直线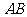 倾斜角的大小。
倾斜角的大小。
冀州中学2009-2010学年高三年级第一次仿真考试
21. (本小题满分12分)
已知函数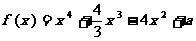
(Ⅰ)求函数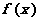 的极大值;
的极大值;
(Ⅱ)当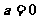 时,求函数
时,求函数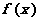 的值域;
的值域;
(Ⅲ)已知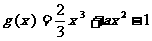 ,当
,当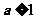 时,
时,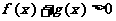 恒成立,求
恒成立,求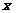 的取值范围.
的取值范围.
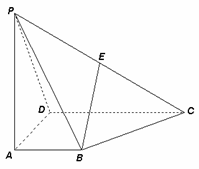
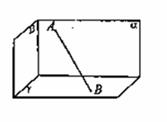
20.(本小题满分12分)如图,四棱锥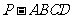 的底面
的底面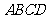 为一直角梯形,其中
为一直角梯形,其中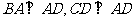 ,
,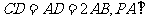 底面
底面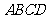 ,
,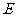 是
是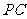 的中点.
的中点.
 (1)求证:
(1)求证: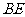 //平面
//平面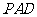 ;
;
(2)若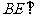 平面
平面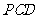 ,
,
①求异面直线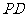 与
与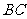 所成角的余弦值;
所成角的余弦值;
②求二面角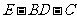 的余弦值
的余弦值
18.(本小题满分12分)
在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球5个,白球3个,蓝球2个.现从中任取出一球确定颜色后放回盒子里,再取下一个球.重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球. 求: (1)最多取两次就结束的概率;
(2)整个过程中恰好取到2个白球的概率; 19. (本小题满分12分)
已知等差数列{an}的首项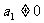 ,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
(1)若a1=2,设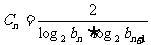 ,求数列{cn}的前n项的和Tn;
,求数列{cn}的前n项的和Tn;
(2)在(1)的条件下,若有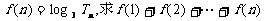 的最大值.
的最大值.
17.(本小题满分10分)已知向量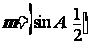
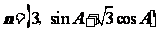 共线,其中A是△ABC的内角.
共线,其中A是△ABC的内角.
(1)求角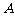 的大小;
的大小;
(2)若BC=2,求△ABC面积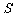 的最大值,并判断S取
的最大值,并判断S取
得最大值时△ABC的形状.
16. 如图,平面
如图,平面 、
、 、
、 两两互相垂直,长为
两两互相垂直,长为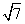 的线段AB在
的线段AB在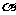 、
、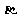 、
、 内的射影的长度分别为
内的射影的长度分别为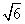 、a、b,则
、a、b,则 的最大值为 .
的最大值为 .
15.观察下列等式:
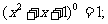
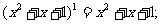

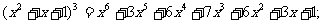 ……;
……;
由此推测,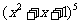 展开式中,第五、六、七项的系数和是
.
展开式中,第五、六、七项的系数和是
.
14. 已知点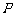 在直线
在直线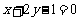 上,点Q在直线
上,点Q在直线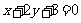 上,PQ的中点为
上,PQ的中点为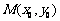 ,且
,且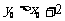 ,则
,则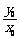 的取值范围是____ ____.
的取值范围是____ ____.
13.一组数据中每个数据都减去80构成一组新数据,这组数据的平均数是1.2,方差是4.4,则原来这组数的平均数和方差分别是 .
12.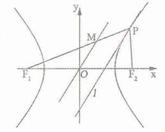 双曲线具有光学性质:“从双曲线的一个焦点发出的光线经过双曲线反射后,反射光线的反向延长线都汇聚到双曲线的另一个焦点。”由此可得如下结论:如右图,过双曲线
双曲线具有光学性质:“从双曲线的一个焦点发出的光线经过双曲线反射后,反射光线的反向延长线都汇聚到双曲线的另一个焦点。”由此可得如下结论:如右图,过双曲线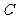 :
: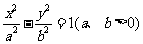 右支上的点
右支上的点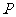 的切线
的切线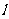 平分
平分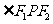 。现过原点作
。现过原点作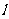 的平行线交
的平行线交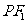 于
于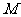 ,则
,则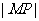 等于
等于
A.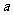 B.
B.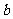 C.
C.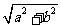 D.与点
D.与点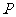 的位置有关
的位置有关
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com