
18.(1)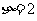 说明2号盒子中可以有1个球或两个球或3个球
说明2号盒子中可以有1个球或两个球或3个球
所以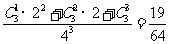
(2)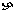 所能取到的值为1,2,3,4
所能取到的值为1,2,3,4
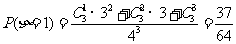
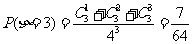
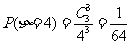 所以分布列为:表格略 期望
所以分布列为:表格略 期望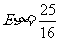
17.(1)因为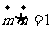 ,所以
,所以
即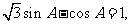 即
即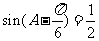
因为0<A<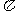 ,则
,则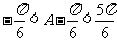 ,所以
,所以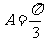
(2)由题知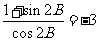 ,得
,得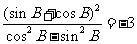 ,即
,即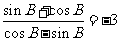
得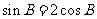 ,即
,即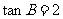
所以,tanC=tan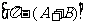 =
=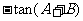
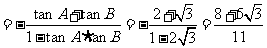
1-5:DBCBC 6-10:ABAAA 11-12:CD
二:填空题
13. 5 14. 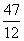 15
15 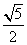 16. 32
16. 32
22. (本小题满分12分)(注意:在试题卷上作答无效)
已知焦点为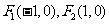 的椭圆经过点
的椭圆经过点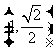 , 直线
, 直线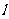 过点
过点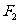 与椭圆交于
与椭圆交于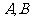 两点, 其中
两点, 其中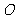 为坐标原点.
为坐标原点.
(1) 求椭圆的方程; (2) 求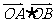 的范围;
的范围;
(3) 若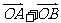 与向量
与向量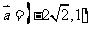 共线, 求
共线, 求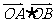 的值及
的值及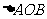 的外接圆方程.
的外接圆方程.
2010年高考模拟冲刺试题答案
21. (本小题满分12分)(注意:在试题卷上作答无效)
已知数列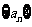 中,
中,  在
在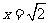 处取得极值.
处取得极值.
(1) 证明数列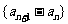 是等比数列, 并求出数列
是等比数列, 并求出数列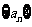 的通项公式;
的通项公式;
(2) 记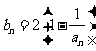 , 数列
, 数列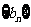 的前
的前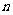 项和为
项和为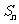 , 求使
, 求使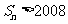 的
的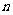 的最小值;
的最小值;
(3) 是否存在指数函数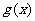 , 使得对于任意正整数
, 使得对于任意正整数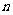 , 都有
, 都有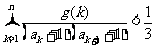 成立, 若存在, 求出满足条件的一个指数函数
成立, 若存在, 求出满足条件的一个指数函数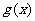 , 若不存在, 请说明理由. ( 其中:
, 若不存在, 请说明理由. ( 其中: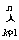 表示
表示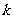 从1到
从1到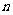 的各项和)
的各项和)
20. (本小题满分12分)(注意:在试题卷上作答无效)
已知函数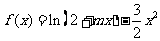 .
.
(1) 若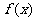 在
在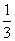 处取得极值, 求
处取得极值, 求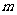 的值;
的值;
(2) 若以函数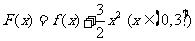 图象上任意一点
图象上任意一点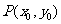 为切点的切线的斜率
为切点的切线的斜率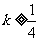 恒成立, 求正实数
恒成立, 求正实数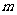 的最小值;
的最小值;
(3) 在(1)的条件下, 若关于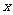 的方程
的方程 在
在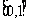 上恰有两个不同的实根, 求实数
上恰有两个不同的实根, 求实数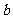 的取值范围.
的取值范围.
19. (本小题满分12分)(注意:在试题卷上作答无效)
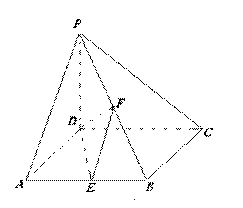 如图,在四棱锥
如图,在四棱锥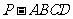 中,
中,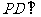 底面
底面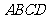 ,底面
,底面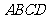 为正方形,
为正方形,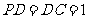 ,
,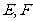 分别是
分别是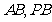 的中点.
的中点.
(1) 求证: 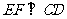 ;
;
(2) 求二面角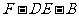 的大小;
的大小;
(3) 在平面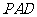 内求一点
内求一点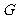 , 使
, 使
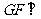 平面
平面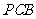 , 并证明你的结论.
, 并证明你的结论.
18. (本小题满分12分)(注意:在试题卷上作答无效)
有3个不相同的球和4个盒子,盒子的编号分别为1、2、3、4,将球逐个独立地、随机地放入4个盒子中去. 以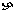 表示其中至少有球的盒子的最小号码.(例如,事件
表示其中至少有球的盒子的最小号码.(例如,事件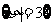 表示第1号,第2号盒子都是空的, 第3号盒子中至少有一个球).
表示第1号,第2号盒子都是空的, 第3号盒子中至少有一个球).
(1) 当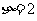 时, 求
时, 求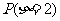 ; (2) 求
; (2) 求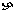 的分布列及期望
的分布列及期望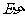 .
.
17. (本小题满分10分)(注意:在试题卷上作答无效)
已知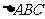 的内角
的内角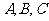 分别对应
分别对应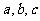 ,向量
,向量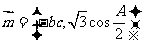
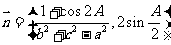 ,且
,且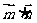 =1.
=1.
(1) 求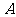 ;
;
(2) 若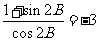 , 求
, 求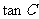 .
.
16. 半径为4的球面上有A,B,C,D四个点, 且满足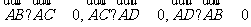 , 则
, 则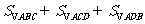 的最大值为
的最大值为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com