
21.本题有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分。如果多做。则按所做的前两题计分
(1)(矩阵与变换)已知矩阵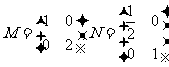 ,矩阵MN对应的变换把曲线
,矩阵MN对应的变换把曲线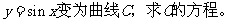
(2)(极坐标与参数方程)已知直线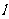 经过点
经过点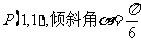 ,
,
①写出直线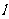 的参数方程;
的参数方程;
②设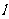 与圆
与圆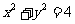 相交于两点
相交于两点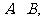 求点
求点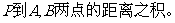
(3)(不等式选讲)设函数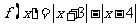
①解不等式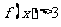 ;
;
②求函数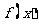 的最小值。
的最小值。
20.(14分)已知函数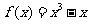
(I)求曲线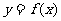 在
在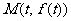 处的切线方程。
处的切线方程。
(II)设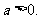 如果过点
如果过点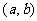 可作曲线
可作曲线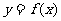 的三条切线,证明:
的三条切线,证明: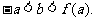
19.(13分)椭圆C的中心为坐标原点O,焦点在y轴上,短轴长为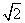 、离心率为
、离心率为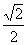 ,直线
,直线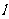 与y轴交于点P(0,
与y轴交于点P(0,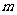 ),与椭圆C交于相异两点A、B,且
),与椭圆C交于相异两点A、B,且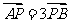 。
。
(I)求椭圆方程;
(II)求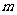 的取值范围。
的取值范围。
18.(13分)祖国大陆开放台湾农民到大陆创业以来,在11个省区设立了海峡两岸农业合作试验区和台湾农民创业园,台湾农民在那里申办个体工商户可以享受“绿色通道”的申请、受理、审批一站式服务。某台商到大陆一创业园投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元.设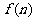 表示前n年的纯收入(
表示前n年的纯收入(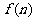 =前n年的总收入-前n前的总支出-投资额)
=前n年的总收入-前n前的总支出-投资额)
(I)从第几年开始获取纯利润?
(II)若干年后,该台商为开发新项目,有两种处理方案:①年平均利润最大时以48万元美元出售该厂;②纯利润总和最大时,以16万美元出售该厂,问哪种方案最合算?
16.(13分)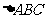 的内角
的内角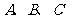 的对边分别为
的对边分别为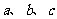 ,三边长
,三边长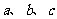 成等比数列。
成等比数列。
(I)若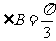 ,求证
,求证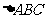 为正三角形;
为正三角形;
(II)若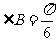 ,求
,求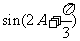 的值。
的值。
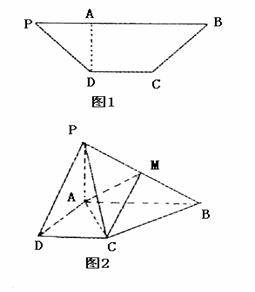 17.(13分)已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=
17.(13分)已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=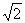 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2)
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2)
(I)证明:平面PAD⊥PCD;
(II)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分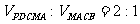 ;
;
(III)在M满足(Ⅱ)的情况下,判断直线AM
是否平行面PCD。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com