3．关注学生用差分方程解决实际问题的能力。特别应鼓励学生能从实际问题建立差分方程，并能结合实际问题引导学生讨论解的实际意义。

2．通过对一阶线性差分方程的讨论，使学生理解方程解的结构，即通解、特解以及与齐次方程通解的关系。这不仅仅是为了求解差分方程，而且对将来进一步学习线性方程组、常微分方程等内容都有所帮助。

1．教学过程和教材编写，应通过大量实例，帮助学生理解差分的概念和差分方程的意义，力求深入浅出。

6．完成一个学习总结报告。报告应包括三方面的内容：(1)知识的总结。对本专题内容的整体结构和内容的理解，对刻画离散变量变化的数学方法的认识。(2)拓展。通过查阅资料、调查研究、访问求教、独立思考，进一步探讨差分方程及其应用。(3)对本专题学习的感受。

　说明与建议

5．应用

　(1)学会用差分方程和差分方程组解决一些简单的实际问题。

　(2)初步体会连续变量离散化的思想，能用它来讨论一些简单的问题。

4．通过具体实例(如种群增长等)，体会方程x_n+1=kx_n(1-x_n)是十分有用的数学模型。借助计算工具，用迭代法分别对k取一些特殊值(如0<k≤1，1<k≤3，k=3.4，k=3.55，k=3.7)的情形,讨论xn的变化，初步了解非线性问题的复杂性。

3．(二元)一阶线性差分方程组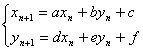

　(1)通过一些实例，认识一阶线性差分方程组是描述现实世界的一个重要模型。

　(2)了解一阶线性差分方程组的通解、特解与其相应齐次方程组通解的关系。

　(3)给定初值，会用迭代法求一阶线性差分方程组的解；能写出求解的算法框图。

　(4)对给定的具体方程组，能初步讨论当n→∞时，解(数列)的变化趋势(收敛、发散、周期)。

2．一阶线性差分方程x_n+1=kx_n+b

　(1)通过一些具体实例，体会方程x_n+1=kx_n+b是十分有用的数学模型。

　(2)理解方程x_n+1=kx_n+b中，当b=0(即方程为齐次方程)时，其解为等比数列；当k=1(即差分为常数)时，其解为等差数列。

　(3)认识方程x_n+1=kx_n+b的通解、特解，了解方程的解与相应的齐次方程x_n+1=kx_n通解的关系；能给出方程x_n+1=kx_n+b的通解公式。

1．数列的差分

　(1)通过一些具体实例，理解数列差分的概念。

　(2)理解数列的一、二阶差分以及它们对描述数列变化的意义，结合数列(作为函数)的图象，了解差分与数列的增减、极值、数列图象的凹凸的关系。

6．这部分内容的教学应让学生认识到，矩阵从实际生活需要中产生，并在实际的问题中有着广泛的应用，体验数学的抽象更有助于人们对问题的思考与解决。

　数列与差分

　随着信息技术的日益普及和发展，离散数学的应用越来越广泛。差分和差分方程是描述离散变量变化的重要工具，在理论上是十分重要的，并且有广泛的应用。

　本专题初步研究数列的差分和简单的差分方程，使学生掌握一些用离散变量分析解决问题的方法。

　内容与要求