
23.(2010陕西省)如图,在RT△ABC中∠ABC=90°,斜边AC的垂直平分线交BC与D点,交AC与E点,连接BE
(1)若BE是△DEC的外接圆的切线,求∠C的大小?
(2)当AB=1,BC=2是求△DEC外界圆的半径
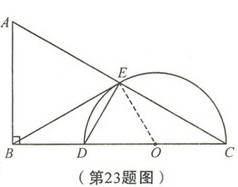
解:(1)∵ DE 垂直平分AC
∴∠DEC=90°
∴DC 为△DEC外接圆的直径
∴DC的中点 O即为圆心
连结OE又知BE是圆O的切线
∴∠EBO+∠BOE=90°
在RT△ABC 中 E 斜边AC 的中点
∴BE=EC
∴∠EBC=∠C
又∵∠BOE=2∠C
∴∠C+2∠C=90°
∴∠C=30°
(2)在RT△ABC中AC= 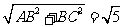 ∴EC=
∴EC=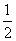 AC=
AC=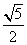
∵∠ABC=∠DEC=90° ∴△ABC∽△DEC
∴ 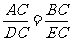 ∴DC=
∴DC=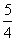
△
DEC 外接圆半径为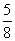
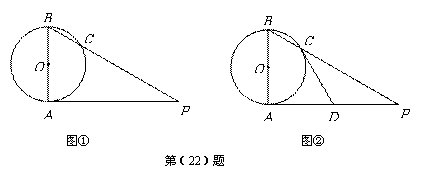
(2010年天津市)(22)(本小题8分)
已知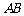 是⊙
是⊙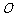 的直径,
的直径,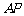 是⊙
是⊙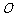 的切线,
的切线,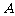 是切点,
是切点,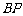 与⊙
与⊙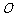 交于点
交于点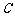 .
.
(Ⅰ)如图①,若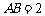 ,
,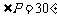 ,求
,求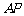 的长(结果保留根号);
的长(结果保留根号);
 (Ⅱ)如图②,若
(Ⅱ)如图②,若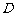 为
为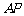 的中点,求证直线
的中点,求证直线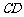 是⊙
是⊙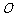 的切线.
的切线.
解:(Ⅰ)∵ 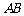 是⊙
是⊙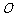 的直径,
的直径,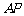 是切线,
是切线,
∴ 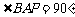 .
.
在Rt△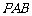 中,
中,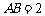 ,
,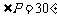 ,
,
∴ 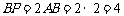 .
.
由勾股定理,得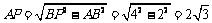 . ..................5分
. ..................5分
(Ⅱ)如图,连接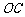 、
、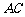 ,
,
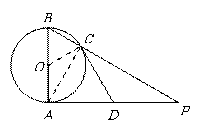 ∵
∵ 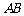 是⊙
是⊙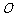 的直径,
的直径,
∴ 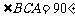 ,有
,有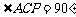 .
.
在Rt△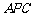 中,
中,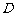 为
为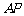 的中点,
的中点,
∴ 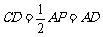 .
.
∴ 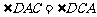 .
.
又 ∵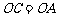 ,
,
∴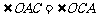 .
.
∵ 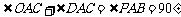 ,
,
∴ 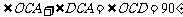 .
.
即 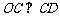 .
.
∴ 直线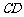 是⊙
是⊙ 的切线. ..............................8分
的切线. ..............................8分
(2010山西22.(本题8分)如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45º.
(1)试判断CD与⊙O的关系,并说明理由.
(2)若⊙O的半径为3cm,AE=5 cm.求∠ADE的正弦值.



1、(2010年杭州市)如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移
动的速度为30千米/时,受影响区域的半径为200千米,B市位
于点P的北偏东75°方向上,距离点P 320千米处.
(1) 说明本次台风会影响B市;
(2)求这次台风影响B市的时间. 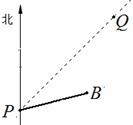
答案:(1) 作BH⊥PQ于点H, 在Rt△BHP中,
由条件知, PB = 320, ÐBPQ = 30°, 得 BH = 320sin30° = 160 < 200, 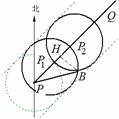
∴ 本次台风会影响B市.
(2) 如图, 若台风中心移动到P1时, 台风开始影响B市, 台风中心移动到P2时, 台风影响结束.
由(1)得BH = 160, 由条件得BP1=BP2 = 200,
∴所以P1P2 = 2 =240,
=240,
∴台风影响的时间t = 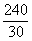 =
8(小时).
=
8(小时).
15.(10重庆潼南县)如图,在矩形ABCD中,AB=6 ,BC=4,⊙O是以AB为直径的圆,则直线DC与⊙O的位置关系是______.相离

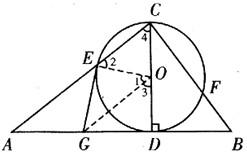
24.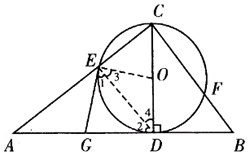 证明:(证法一)连接
证明:(证法一)连接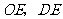 .
1分
.
1分
∵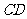 是⊙O的直径,
是⊙O的直径,
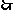
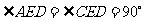 . 2分
. 2分
∵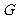 是
是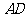 的中点,
的中点,
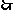
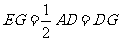 . 4分
. 4分
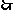
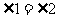 . 6分
. 6分
∵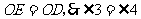 . 8分
. 8分
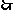
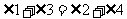 .即
.即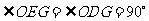 . 10分
. 10分
 是⊙O的切线. 12分
是⊙O的切线. 12分
(证法二)连接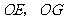 . 1分
. 1分
∵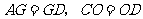 ,
,
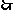
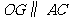 . 2分
. 2分
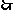
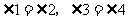 . 4分
. 4分
∵OC=OE.
∴∠2=∠4.
∴∠1=∠3. 6分
又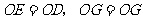 ,
,
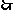
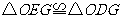 . 8分
. 8分
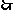
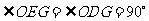 . 10分
. 10分
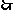
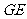 是⊙O的切线. 12分
是⊙O的切线. 12分
4.(2010年眉山)⊙O1的半径为3cm,⊙O2的半径为5cm,圆心距O1O2=2cm,这两圆的位置关系是
A.外切 B.相交 C.内切 D.内含
答案:C
毕节24.(本题12分)如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA、CB于点E、F,点G是AD的中点.求证:GE是⊙O的切线.
8.(2010年成都)已知两圆的半径分别是4和6,圆心距为7,则这两圆的位置关系是( )
(A)相交 (B)外切 (C)外离 (D)内含
答案:A
6.(2010年长沙)已知⊙O1、⊙O2的半径分别是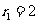 、
、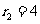 ,若两圆相交,则圆心距O1O2可能取的值是 B
,若两圆相交,则圆心距O1O2可能取的值是 B
A.2 B.4 C.6 D.8
13. (2010年金华) 如果半径为3cm的⊙O1与半径为4cm的⊙O2内切,那么两圆的圆心距O1O2= ▲ cm.
答案:1;
6.(2010宁波市)两圆的半径分别为3和5,圆心距为7,则两圆的位置关系是
A.内切 B.相交 C.外切 D.外离
26.(2010年兰州)(本题满分10分)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)求证:BC=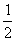 AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
答案(本题满分10分)
解:(1)∵OA=OC,∴∠A=∠ACO
∵∠COB=2∠A ,∠COB=2∠PCB
∴∠A=∠ACO=∠PCB ……………………………………………………1分
∵AB是⊙O的直径
∴∠ACO+∠OCB=90° …………………………………………………2分
∴∠PCB+∠OCB=90°,即OC⊥CP …………………………………………3分
∵OC是⊙O的半径
∴PC是⊙O的切线 …………………………………………………4分
(2)∵PC=AC ∴∠A=∠P
∴∠A=∠ACO=∠PCB=∠P
∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB
∴∠CBO=∠COB ……………………………………………5分
∴BC=OC
∴BC=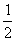 AB
………………………………………………………6分
AB
………………………………………………………6分
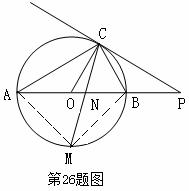 (3)连接MA,MB
(3)连接MA,MB
∵点M是弧AB的中点
∴弧AM=弧BM ∴∠ACM=∠BCM ………7分
∵∠ACM=∠ABM ∴∠BCM=∠ABM
∵∠BMC=∠BMN
∴△MBN∽△MCB
∴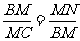
∴BM2=MC·MN ……………………8分
∵AB是⊙O的直径,弧AM=弧BM
∴∠AMB=90°,AM=BM
∵AB=4 ∴BM=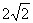 ………………………………………………………9分
………………………………………………………9分
∴MC·MN=BM2=8 ……………………………………………………10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com