23．(2010河北省)(本小题满分10分)

观察思考

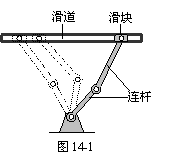
某种在同一平面进行传动的机械装置如图14-1，图14-2

是它的示意图．其工作原理是：滑块Q在平直滑道l上可以

左右滑动，在Q滑动的过程中，连杆PQ也随之运动，并且

PQ带动连杆OP绕固定点O摆动．在摆动过程中，两连杆的接点P在以OP为半径的⊙O上运动．数学兴趣小组为进一步研

究其中所蕴含的数学知识，过点O作OH　⊥l于点H，并测得

OH　=　4分米，PQ　=　3分米，OP　=　2分米．

解决问题

(1)点Q与点O间的最小距离是　　　　 分米；

点Q与点O间的最大距离是　　　　 分米；

点Q在l上滑到最左端的位置与滑到最右端位置间

的距离是　　　　 分米．

(2)如图14-3，小明同学说：“当点Q滑动到点H的位

置时，PQ与⊙O是相切的．”你认为他的判断对吗？

为什么？

(3)①小丽同学发现：“当点P运动到OH上时，点P到l

的距离最小．”事实上，还存在着点P到l距离最大

的位置，此时，点P到l的距离是　　　　 分米；

②当OP绕点O左右摆动时，所扫过的区域为扇形，

求这个扇形面积最大时圆心角的度数．

解：(1)4　　 5　　 6；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

(2)不对．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

∵OP　=　2，PQ　=　3，OQ　=　4，且4²≠3²+　2²，即OQ²≠PQ²+　OP²，

∴OP与PQ不垂直．∴PQ与⊙O不相切．

(3)① 3；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

②由①知，在⊙O上存在点P，到l的距离为3，此时，OP将不能再向下转动，如图3．OP在绕点O左右摆动过程中所扫过的最大扇形就是OP．

连结P，交OH于点D．

∵PQ，均与l垂直，且PQ　=，

∴四边形PQ是矩形．∴OH⊥P，PD =D．

由OP　=　2，OD　=　OH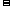HD　=　1，得∠DOP　=　60°．

∴∠PO　=　120°．

∴ 所求最大圆心角的度数为120°．

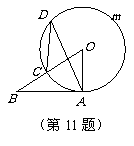(2010河南)11．如图，AB切⊙O于点A，BO交⊙O于点C，点D是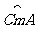上异于点C、A的一点，若∠ABO=32°，则∠ADC的度数是______________．

29°

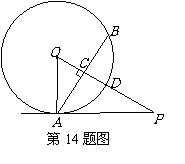(2010广东中山)14．如图，PA与⊙O相切于A点，弦AB⊥OP，垂足为C，OP与⊙O相交于D点，已知OA=2，OP=4。

(1)求∠POA的度数；

(2)计算弦AB的长。

15．(2010株洲市)两圆的圆心距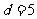，它们的半径分别是一元二次方程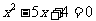的两个根，这两圆的位置关系是　　　　　 外切　　　 .

6.(2010年常州)若两圆的半径分别为2和3，圆心距为5，则两圆的位置关系为

A.外离　　　　 B.外切　　　　　 C.相交　　　　 D.内切

2、C

3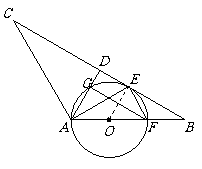．(1)证明：连接OE，------------------------------1分

∵AB=AC且D是BC中点，

∴AD⊥BC．

∵AE平分∠BAD，

∴∠BAE=∠DAE．------------------------------3分

∵OA=OE，

∴∠OAE=∠OEA．

∴∠OEA=∠DAE．

∴OE∥AD．

∴OE⊥BC．

∴BC是⊙O的切线．---------------------------6分

(2)∵AB=AC，∠BAC=120°，

∴∠B=∠C=30°．----------------------------7分

∴∠EOB =60°．------------------------------8分

∴∠EAO =∠EAG =30°．-------------------9分

∴∠EFG =30°．------------------------------10分

3．(2010山东德州)

如图，在△ABC中，AB=AC，D是BC中点，AE平分∠BAD交BC于点E，点O是AB上一点，⊙O过A、E两点, 交AD于点G，交AB于点F．

(1)求证：BC与⊙O相切；

(2)当∠BAC=120°时，求∠EFG的度数．

答案：1．A

2．(2010山东德州)已知三角形的三边长分别为3,4,5，则它的边与半径为1的圆的公共点个数所有可能的情　 况是

(A)0，1，2，3　　 (B)0，1，2，4　 (C)0，1，2，3，4　　 (D)0，1，2，4，5

1．(2010四川宜宾)若⊙O的半径为4cm，点A到圆心O的距离为3cm，那么点A与⊙O的位置关系是(　　 )

A．点A在圆内　　 B．点A在圆上　　 C．点A在圆外　　 D．不能确定

1．(2010山东济南)

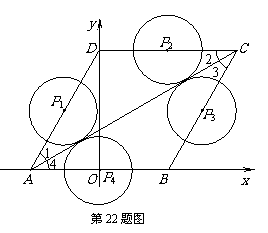
如图所示，菱形ABCD的顶点A、B在x轴上，点A在点B的左侧，点D在y轴的正半轴上，∠BAD=60°，点A的坐标为(－2，0)．

⑴求线段AD所在直线的函数表达式．

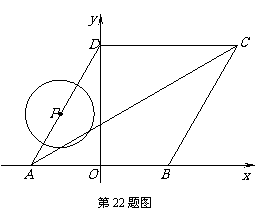⑵动点P从点A出发，以每秒1个单位长度的速度，按照A→D→C→B→A的顺序在菱形的边上匀速运动一周，设运动时间为t秒．求t为何值时，以点P为圆心、以1为半径的圆与对角线AC相切？

答案：1 解：⑴∵点A的坐标为(－2，0)，∠BAD=60°，∠AOD=90°，

∴OD=OA·tan60°=，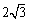

∴点D的坐标为(0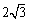，)，························································ 1分

设直线AD的函数表达式为，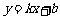

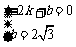，解得，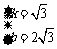

∴直线AD的函数表达式为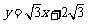. ···································· 3分

⑵∵四边形ABCD是菱形，

∴∠DCB=∠BAD=60°，

∴∠1=∠2=∠3=∠4=30°，

　 AD=DC=CB=BA=4，···································································· 5分

如图所示：

①点P在AD上与AC相切时，

AP₁=2r=2，

∴t₁=2. ·························································································· 6分

②点P在DC上与AC相切时，

CP₂=2r=2，

∴AD+DP₂=6，

∴t₂=6. ··································· 7分

③点P在BC上与AC相切时，

CP₃=2r=2，

∴AD+DC+CP₃=10，

∴t₃=10.··································· 8分

④点P在AB上与AC相切时，

AP₄=2r=2，

∴AD+DC+CB+BP₄=14，

∴t₄=14，

∴当t=2、6、10、14时，以点P为圆心、以1为半径的圆与对角线AC相切.

······················································ 9分

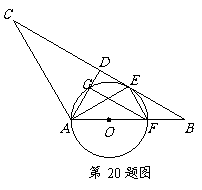
2.(2010黄冈)6分)如图，点P为△ABC的内心，延长AP交△ABC的外接圆于D，在AC延长线上有一点E，满足AD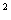＝AB·AE，求证：DE是⊙O的切线.

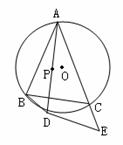
　　　　　　　　　　　　第20题图

证明：连结DC，DO并延长交⊙O于F，连结AF.∵AD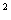＝AB·AE，∠BAD＝∠DAE，∴△BAD∽△DAE，∴∠ADB＝∠E.　又∵∠ADB＝∠ACB，∴∠ACB＝∠E，BC∥DE，∴∠CDE＝∠BCD＝∠BAD＝∠DAC，又∵∠CAF＝∠CDF，∴∠FDE＝∠CDE+∠CDF＝∠DAC+∠CDF＝∠DAF＝90°，故DE是⊙O的切线

1.(2010宁德)．如图，在8×4的方格(每个方格的边长为1个单位长)中，⊙A的

半径为1，⊙B的半径为2，将⊙A由图示位置向右平移1个单位长后，

⊙A与静止的⊙B的位置关系是(　　 )．D

A.内含　　　 　B.内切　　　 　C.相交　　　　 D.外切