
5.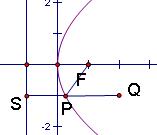 (2008年海南理11)已知点P在抛物线
(2008年海南理11)已知点P在抛物线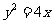 上,那么点P到点
上,那么点P到点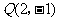 的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
A.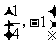 B.
B.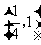 C.
C.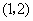 D.
D.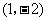
解:点P到抛物线焦点距离等于点P到抛物线准线距离,如图
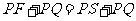 ,故最小值在
,故最小值在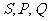 三点共线时取得,
三点共线时取得,
此时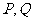 的纵坐标都是
的纵坐标都是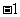 ,所以选A。(点
,所以选A。(点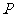 坐标为
坐标为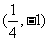 )
)
4.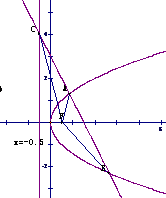 (2009年天津理9)设抛物线
(2009年天津理9)设抛物线 =2x的焦点为F,过点M(
=2x的焦点为F,过点M(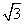 ,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,
,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,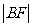 =2,则
=2,则 BCF与
BCF与 ACF的面积之比
ACF的面积之比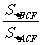 =
=
(A)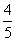 (B)
(B)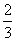 (C)
(C)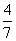 (D)
(D)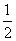
[考点定位]本小题考查抛物线的性质、三点共线的坐标关系,和综合运算数学的能力,中档题。
解析:由题知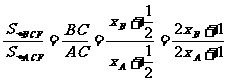 ,
,
又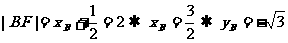
由A、B、M三点共线有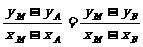 即
即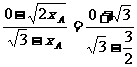 ,故
,故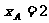 ,
, 
∴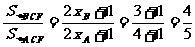 ,故选择A。
,故选择A。
3.( 2010年辽宁理7)设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如果直线AF的斜率为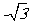 ,那么|PF|=
,那么|PF|=
(A)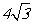 (B)8 (C)
(B)8 (C) (D)
16
(D)
16
[答案]B[解析]抛物线的焦点F(2,0),直线AF的方程为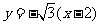 ,所以点
,所以点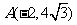 、
、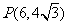 ,从而|PF|=6+2=8
,从而|PF|=6+2=8
2.(2010年福建理2)以抛物线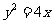 的焦点为圆心,且过坐标原点的圆的方程为( )
的焦点为圆心,且过坐标原点的圆的方程为( )
A.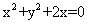 B.
B. 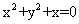 C.
C. 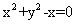 D.
D. 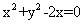
[答案]D[解析]因为已知抛物线的焦点坐标为(1,0),即所求圆的圆心,又圆过原点,所以圆的半径为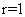 ,故所求圆的方程为
,故所求圆的方程为 ,即
,即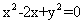 ,选D。
,选D。
[命题意图]本题考查抛物线的几何性质以及圆的方程的求法,属基础题。
1.(2010年陕西理8).已知抛物线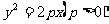 的准线与圆
的准线与圆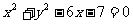 相切,则
相切,则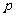 的值为 [ ]
的值为 [ ]
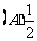
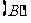
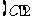
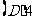
[答案]C[解析]由题设知,直线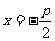 与圆
与圆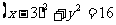 相切,从而
相切,从而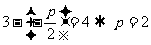 .故选
.故选 .
.
19、曙光公司为了打开某种新产品的销路,决定进行广告促销,在一年内,预计年销量Q(万件)与广告费x(万元)之间的函数关系式是Q= 已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需投入32万元,若每件售价是“年平均每件成本的150%”与“年平均每件所占广告费的50%”之和,当年产销量相等试将年利润y(万元)表示为年广告费x万元的函数,并判断当年广告费投入100万元时,该公司是亏损还是盈利?
已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需投入32万元,若每件售价是“年平均每件成本的150%”与“年平均每件所占广告费的50%”之和,当年产销量相等试将年利润y(万元)表示为年广告费x万元的函数,并判断当年广告费投入100万元时,该公司是亏损还是盈利?
18、求函数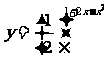 的值域和单调区间
的值域和单调区间
17、若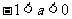 ,则
,则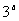 ,
,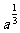 ,
,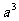 由大到小的顺序是____________
由大到小的顺序是____________
16、若点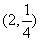 既在函数
既在函数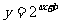 的图象上,又在它的反函数的图象上,则
的图象上,又在它的反函数的图象上,则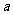 =__________________,
=__________________,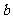 =__________________
=__________________
15、函数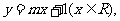 与
与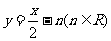 互为反函数的充要条件是___________
互为反函数的充要条件是___________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com