
正解:z=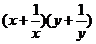 =
=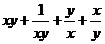 =
=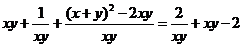 ,令t=xy, 则
,令t=xy, 则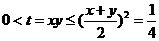 ,由
,由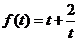 在
在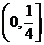 上单调递减,故当t=
上单调递减,故当t=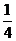 时
时 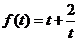 有最小值
有最小值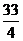 ,所以当
,所以当 时z有最小值
时z有最小值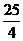 。
。
错解分析:解一等号成立的条件是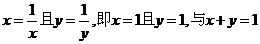 相矛盾。解二等号成立的条件是
相矛盾。解二等号成立的条件是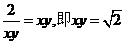 ,与
,与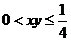 相矛盾。
相矛盾。
3.(如中)已知两正数x,y 满足x+y=1,则z=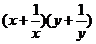 的最小值为
。
的最小值为
。
错解:不能灵活运用平均数的关系,正解:由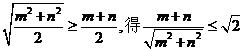 ,即
,即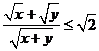 ,故a的最小值是
,故a的最小值是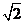 。
。
2.(如中)若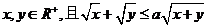 恒成立,则a的最小值是
恒成立,则a的最小值是
错解:有消元意识,但没注意到元的范围。正解:由 得:
得: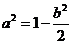 ,且
,且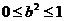 ,原式=
,原式=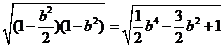 ,求出最大值为1。
,求出最大值为1。
1.(如中)设 ,则
,则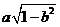 的最大值为
的最大值为
A、0≤m≤1
B、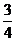 <m≤1 C、
<m≤1 C、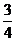 ≤m≤1 D、m≥
≤m≤1 D、m≥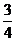
正确答案:(B)
错误原因:不能充分挖掘题中隐含条件。
二填空题:
24.(案中)如果方程(x-1)(x 2-2x+m)=0的三个根可以作为一个三角形的三条边长,那么实数m的取值范围是 ( )
错因:忽视基本不等式使用的条件,而用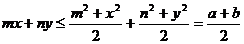 得出错解。
得出错解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com