
24、(上海市部分重点中学2008届高三第二次联考)电信局根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,则两种方案付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分)(MN平行CD)
 (1)若通话时间为两小时,按方案A,B各付话费多少元?
(1)若通话时间为两小时,按方案A,B各付话费多少元?
(2)方案B从500分钟以后,每分钟收费多少元?
(3)通话时间在什么范围内,方案B比方案A优惠?
[解]设通话x分钟时,方案A,B的通话费分别为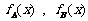 ---------1分
---------1分
(1)当x=120时  =116元
=116元
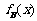 =168元-----------3分
=168元-----------3分
若通话时间为两小时,方案A付话费116元,方案B付话费168元------4分
(2) ----------7分
----------7分
当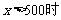
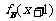 -
-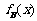 =0.3 --------------------------------9分
=0.3 --------------------------------9分
方案B从500分钟以后,每分钟收费0.3 元-------------------10分
(3) 当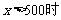
 -------------------------------11分
-------------------------------11分
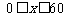
 ----------------------12分
----------------------12分
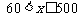 由
由 得
得 ----------13分
----------13分
综合:通话时间在 内方案B较优惠。----------14分
内方案B较优惠。----------14分
23、(山东省聊城市2008届第一期末统考)某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元.设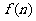 表示前n年的纯利润总和(f(n)=前n年的总收入一前n年的总支出一投资额).
表示前n年的纯利润总和(f(n)=前n年的总收入一前n年的总支出一投资额).
(1)该厂从第几年开始盈利?
(2)若干年后,投资商为开发新项目,对该厂有两种处理方案:①年平均纯利润达到最大时,以48万元出售该厂;②纯利润总和达到最大时,以16万元出售该厂,问哪种方案更合算?
解:由题意知
 ………………2分
………………2分
(1)由 …………5分
…………5分
由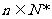 知,从经三年开始盈利.…………………………6分
知,从经三年开始盈利.…………………………6分
(2)方案①:年平均纯利润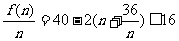
当且仅当n=6时等号成立.
故方案①共获利6×16+48=144(万元),此时n=6.………………8分
方案②: 当n=10,
当n=10,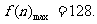
故方案②共获利128+16、144(万元)……………………10分
比较两种方案,获利都是144万元,但由于第①种方案只需6年,而第②种方案需10年,故选择第①种方案更合算.…………………………12分
22、(本小题满分12分)(江苏省南通通州市2008届高三年级第二次统一测试) 某学校拟建一块周长为400m的操场如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽?
某学校拟建一块周长为400m的操场如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽?
解:设矩形的长为xm,半圆的直径是d,中间的矩形区域面积为Sm2.
由题知:S=dx,且2x+πd=400 2′
∴S= 5′
5′
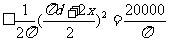 10′
10′
当且仅当πd=2x=200,即x=100时等号成立
设计矩形的长为100m宽约为63.7m时,矩形面积最大. 12′
21、(江苏省泰兴市2007-2008学年第一学期高三调研)设a、b、c均为实数,求证: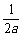 +
+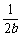 +
+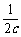 ≥
≥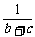 +
+ +
+ .
.
证明: ∵a、b、c均为实数,
∴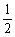 (
(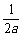 +
+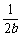 )≥
)≥ ≥
≥ ,当a=b时等号成立;……………………4分
,当a=b时等号成立;……………………4分
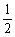 (
(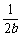 +
+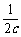 )≥
)≥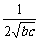 ≥
≥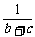 ,当b=c时等号成立;……………………6分
,当b=c时等号成立;……………………6分
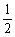 (
(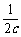 +
+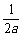 )≥
)≥ ≥
≥ .……………………8分
.……………………8分
三个不等式相加即得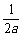 +
+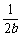 +
+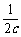 ≥
≥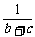 +
+ +
+ ,
,
当且仅当a=b=c时等号成立. ……………………10分
20、(江苏省泰兴市2007-2008学年第一学期高三调研)设函数 求证:
求证:
(1) ;
;
(2)函数 在区间(0,2)内至少有一个零点;
在区间(0,2)内至少有一个零点;
(3)设 是函数
是函数 的两个零点,则
的两个零点,则
证明:(1)

又

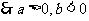 ……………………2分
……………………2分
又2c=-3a-2b 由3a>2c>2b ∴3a>-3a-2b>2b
∵a>0  ………………………………………………4分
………………………………………………4分
(2)∵f(0)=c,f(2)=4a+2b+c=a-c………………………………6分
①当c>0时,∵a>0,∴f(0)=c>0且
∴函数f(x)在区间(0,1)内至少有一个零点……………………8分
②当c≤0时,∵a>0 
∴函数f(x)在区间(1,2)内至少有一个零点.
综合①②得f(x)在(0,2)内至少有一个零点…………………………10分
(3)∵x1,x2是函数f(x)的两个零点
则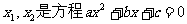 的两根
的两根
∴ ……………………………………12分
……………………………………12分
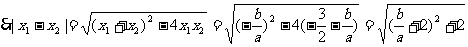

 ……………………………………15分
……………………………………15分
19、(江苏省南通市2008届高三第二次调研考试)已知x,y,z均为正数.求证:
证明:因为x,y,z无为正数.所以 ,
………………………………4分
,
………………………………4分
同理可得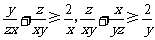 ,………………………………………………………7分
,………………………………………………………7分
当且仅当x=y=z时,以上三式等号都成立.
将上述三个不等式两边分别相加,并除以2,得 .…………10分
.…………10分
18、(吉林省吉林市2008届上期末)已知函数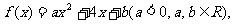 设关于x的方程
设关于x的方程 的两实根为x1、x2,方程
的两实根为x1、x2,方程 的两实根为
的两实根为 .
.
(1)若 =1,求a、b的关系式;
=1,求a、b的关系式;
(2)若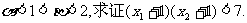
解:(1)由 有两个不等实根为α、β,
有两个不等实根为α、β,
 ……………………………………2分
……………………………………2分
由
 ………………………………6分
………………………………6分
(2)证明: ,
,

则 ……………………10分
……………………10分

综上所述, ……………………………………………………12分
……………………………………………………12分
17、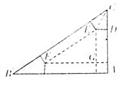 (湖南省长沙市一中2008届高三第六次月考)某加工厂有一块三角形的铁板余料(如图),经测量得知:AC=3,AB=3
(湖南省长沙市一中2008届高三第六次月考)某加工厂有一块三角形的铁板余料(如图),经测量得知:AC=3,AB=3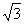 ,BC=6.工人师傅计划用它加工成一个无盖直三棱柱型水箱,设计方案为:将图中的阴影部分切去,再把它沿虚线折起,请计算容器的高为多少时,容器的容积最大?最大容积是多少?
,BC=6.工人师傅计划用它加工成一个无盖直三棱柱型水箱,设计方案为:将图中的阴影部分切去,再把它沿虚线折起,请计算容器的高为多少时,容器的容积最大?最大容积是多少?
解:设容器的高为x.



又GE>0,∴0<x<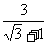
设容器的容积为V.
则V= …………………………………………………………(6分)
…………………………………………………………(6分)

 ……………………………………………………(7分)
……………………………………………………(7分)
令 ,又0<x<
,又0<x<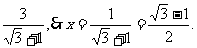 ………………………………(10分)
………………………………(10分)
当0<x<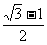 时,
时, .………………………………………(13分)
.………………………………………(13分)
16、(湖北省黄冈中学2008届高三第一次模拟考试)随着机构改革的深入进行,各单位要减员增效,有一家公司现有职员2a人(140<2a<420,且a为偶数),每人每年可创利b万元. 据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.01b万元,但公司需付下岗职员每人每年0.4b万元的生活费,并且该公司正常运转所需人数不得小于现有职员的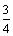 . 为获得最大的经济效益,该公司应裁员多少人?
. 为获得最大的经济效益,该公司应裁员多少人?
解:设裁员x人,可获得的经济效益为y万元,
则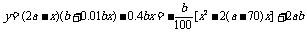 ……4分
……4分
依题意
又140<2a<420, 70<a<210. ……6分
(1)当 时,x=a-70, y取到最大值;……8分
时,x=a-70, y取到最大值;……8分
(2)当 时,
时, ,
y取到最大值;……10分
,
y取到最大值;……10分
答:当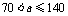 时,裁员a-70人;当
时,裁员a-70人;当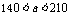 时,裁员
时,裁员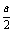 人……12分
人……12分
15、(湖北省鄂州市2008年高考模拟)某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止供应该厂的生产和生活用水,已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间t(小时,且规定早上6时t=0)的函数关系为W=100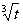 .水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
.水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
解:设进水量选第x级,则t小时后水塔中水的剩余量为:
y=100+10xt-10t-100 ,且0≤t≤16.
,且0≤t≤16.
根据题意0<y≤300,∴0<100+10xt-10t-100 ≤300.
≤300.
当t=0时,结论成立.
当t>0时,由左边得x>1+10( ), 令m=
), 令m=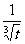 ,由0<t≤16,m ≥
,由0<t≤16,m ≥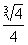 ,
,
记f(t)=1+10( )=1+10m2-10m3,(m ≥
)=1+10m2-10m3,(m ≥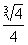 )
)
则f¢(t)=20m – 30 m
2 =0得m = 0或m =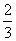 .
.
∵当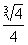 ≤m <
≤m <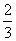 时,f¢(t)>0;当m >
时,f¢(t)>0;当m >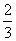 时,f¢(t)<0,
时,f¢(t)<0,
∴所以m =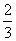 时(此时t =
时(此时t = ),f(t)最大值=1+10(
),f(t)最大值=1+10(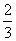 )2-10(
)2-10(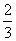 )3=
)3= ≈2.48.
≈2.48.
当t= 时,1+10(
时,1+10( )有最大值2.48.
)有最大值2.48.
∴x>2.48,即x≥3.
由右边得x≤ +1,当t=16时,
+1,当t=16时, +1有最小值
+1有最小值
 +1=
+1= ∈(3,4).即x≤3.
∈(3,4).即x≤3.
综合上述,进水量应选为第3级.
[总结点评]本题考查数学建模的基本思想,怎么样把实际问题转化为数学问题,进而用已有的数学知识求这个数学问题的解。水塔中的水不空又不会使水溢出等到价于进出水量的平衡,进水量与选择的进水级别与进水时间相关,出水量有生活用水与工业用水两部分构成,故水塔中水的存量是一个关于进水级别与用水时间的函数,而容量为300吨的水塔就构成一个不等式,解之得问题的解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com