
6.在等比数列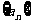 的前n项和中,
的前n项和中,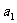 最小,且
最小,且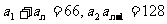 ,前n项和
,前n项和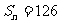 ,则n=_____,公比q=____
,则n=_____,公比q=____
简答.提示:1-4.CBBC;
4.(2004湖北)已知数列{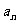 }的前n项和
}的前n项和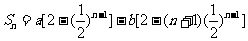 ,
,
(n=1,2,…)其中a、b是非零常数,则存在数列{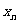 }、{
}、{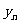 }使得
( )
}使得
( )
A.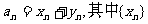 为等差数列,{
为等差数列,{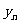 }为等比数列
}为等比数列
B.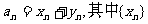 和{
和{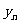 }都为等差数列
}都为等差数列
C.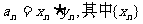 为等差数列,{
为等差数列,{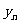 }都为等比数列
}都为等比数列
D.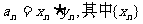 和{
和{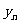 }都为等比数列
}都为等比数列
[填空题] 5.求和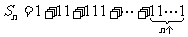 =
=
3.(2004全国)等差数列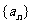 中,
中,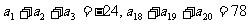 ,则此数列前20项和等于
( )
,则此数列前20项和等于
( )
A.160 B.180 C.200 D.220
2.数列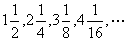 前n项的和为
( )
前n项的和为
( )
A.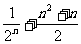 B.
B.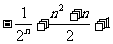
C.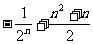 D.
D. 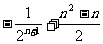
1.数列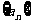 中
中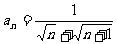 ,若前n项的和为10,则项数n为 ( )
,若前n项的和为10,则项数n为 ( )
A.11 B.99 C.120 D.121
3. 解题时注意转化和有目的的配凑;
同步练习 3.5数列求和
[选择题]
2.利用等比数列求和公式时注意分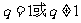 讨论。
讨论。
1.掌握各种求和基本方法;
3.运用等比数列求和公式时,要注意公比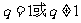 讨论。
讨论。
[例2]求和
解: 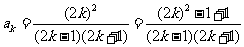
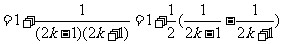
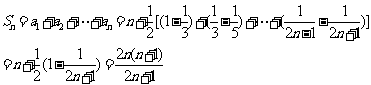
提炼方法:凑分母化简,心中的目标是凑出“等差数列连续两项积的倒数”再裂项相消。
练习:求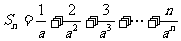 答案:
答案: 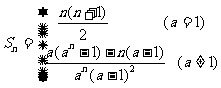
[例3]求证: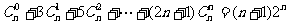
思路分析:由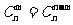 可用倒序相加法求和。
可用倒序相加法求和。
证:令
则
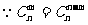
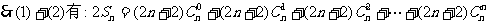
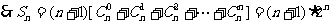 等式成立
等式成立
提炼方法:与推导等差数列求和公式一样,倒序相加,凑出特殊数列求和。此外还可用归纳猜想法,奇偶法等方法求和。
[例4](2005全国1)设等比数列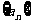 的公比为
的公比为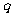 ,前n项和
,前n项和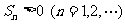
(Ⅰ)求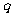 的取值范围;
的取值范围;
(Ⅱ)设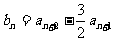 ,记
,记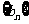 的前n项和为
的前n项和为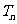 ,试比较
,试比较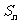 与
与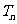 的大小
的大小
解:(Ⅰ)当q>0时显然成立;当q<0时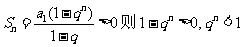 对任意n成立,必有q>-1,故q的取值范围是
对任意n成立,必有q>-1,故q的取值范围是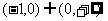
(Ⅱ)∵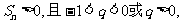
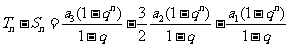
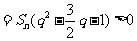 得
得 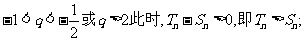
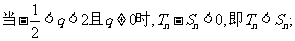
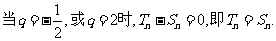
[研讨.欣赏](2006湖北)已知二次函数y=f(x)的图像经过坐标原点,其导函数为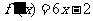 。数列
。数列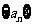 的前n项和为
的前n项和为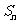 ,点
,点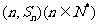 均在函数
均在函数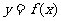 的图像上。(Ⅰ)求数列{an}的通项公式;
的图像上。(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设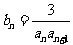 ,
,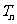 是数列
是数列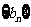 的前n项和,求使得
的前n项和,求使得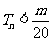 对所有
对所有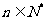 都成立的最小正整数m。
都成立的最小正整数m。
本小题主要考查二次函数、等差数列、数列求和、不等式等基础和基本的运算技能,考查分析问题的能力和推理能力。
解:(I)依题意可设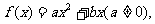 则
则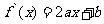
由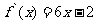 得
得 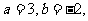 所以
所以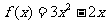
又由点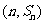
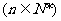 均在函数
均在函数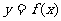 的图像上得
的图像上得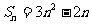
当  时
时
当 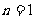 时
时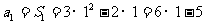
所以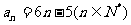
(II)由(I)得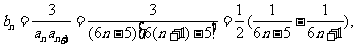
故,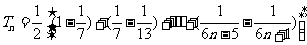 =
=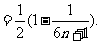
因此使得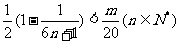 成立的m必须且必须满足
成立的m必须且必须满足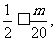 即
即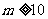
故满足最小的正整数m为10
[例1]求和:①求数列1,3+4,5+6+7,7+8+9+10,…前n项和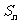
②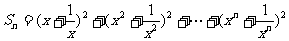
③已知数列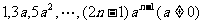 ,求前n项和。
,求前n项和。
④已知数列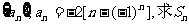 。
。
解:①
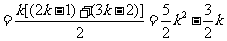
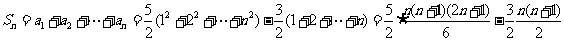
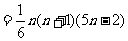
②
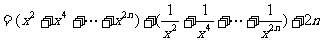
(1)当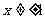 时,
时,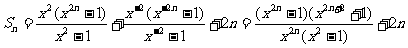
(2)当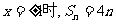
③
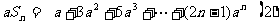
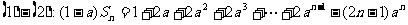
当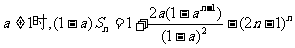
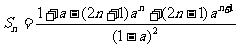
当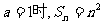
④an=-2n+(-1)n,分两个数列求和得
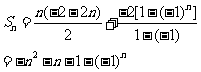
法2:(对n分奇偶讨论求和)
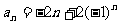 ,若
,若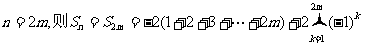
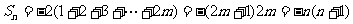
若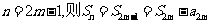
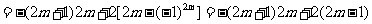
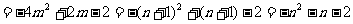
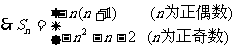
提炼方法:1.通过分组,通过拆并组合,凑出等差等比数列,用公式求和;
2.乘公比,错位相减法求和,用于等差、等比数列对应项的积构成的数列求和.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com