
4、(江苏省启东中学高三综合测试四)已知以向量v=(1, 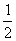 )为方向向量的直线l过点(0,
)为方向向量的直线l过点(0, 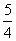 ),抛物线C:
),抛物线C: (p>0)的顶点关于直线l的对称点在该抛物线上.
(p>0)的顶点关于直线l的对称点在该抛物线上.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若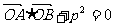 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.
解:(Ⅰ)由题意可得直线l: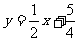 ①
①
过原点垂直于l的直线方程为  ②
②
解①②得 .
.
∵抛物线的顶点关于直线l的对称点在该抛物线的准线上.
∴ ,
,
∴抛物线C的方程为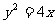 .
.
(Ⅱ)设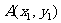 ,
,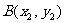 ,
,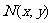 ,
,
由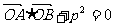 ,得
,得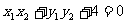 .
.
又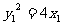 ,
,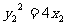 .
.
解得  ③
③
直线ON: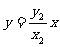 ,即
,即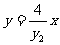 ④
④
由③、④及 得,
得,
点N的轨迹方程为
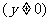 .
.
3、(江苏省启东中学高三综合测试三)(1)在双曲线xy=1上任取不同三点A、B、C,证明:⊿ABC的垂心H也在该双曲线上;
(2)若正三角形ABC的一个顶点为C(―1,―1),另两个顶点A、B在双曲线xy=1另一支上,求顶点A、B的坐标。
解:(1)略;(2)A(2+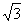 ,2-
,2-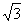 ), B(2-
), B(2-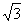 ,2+
,2+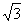 )或A(2-
)或A(2-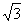 ,2+
,2+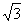 ),
B(2+
),
B(2+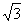 ,2-
,2-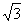 )
)
2、(江苏省启东中学高三综合测试二)已知动圆过定点P(1,0),且与定直线L:x=-1相切,点C在l上.
(1)求动圆圆心的轨迹M的方程;
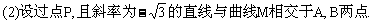
(i)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由
(ii)当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
解:(1)依题意,曲线M是以点P为焦点,直线l为准线的抛物线,所以曲线M的方程为y2=4x.
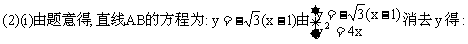
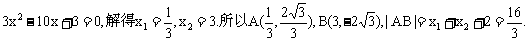
假设存在点C(-1,y),使△ABC为正三角形,则|BC|=|AB|且|AC|=|AB|,即

因此,直线l上不存在点C,使得△ABC是正三角形.
(ii)解法一:设C(-1,y)使△ABC成钝角三角形,
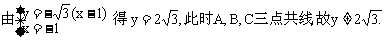 ,
,
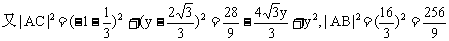 ,
,
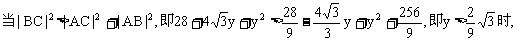
∠CAB为钝角.
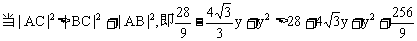
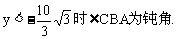

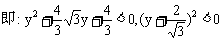 .
.
该不等式无解,所以∠ACB不可能为钝角.
因此,当△ABC为钝角三角形时,点C的纵坐标y的取值范围是:
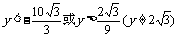 .
.
解法二: 以AB为直径的圆的方程为:
 .
.

当直线l上的C点与G重合时,∠ACB为直角,当C与G 点不重合,且A,
B,C三点不共线时, ∠ACB为锐角,即△ABC中∠ACB不可能是钝角.
因此,要使△ABC为钝角三角形,只可能是∠CAB或∠CBA为钝角.
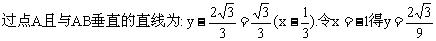 .
.
 .
.
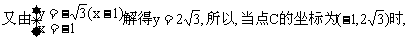
A,B,C三点共 线,不构成三角形.
因此,当△ABC为钝角三角形时,点C的纵坐标y的取值范围是:

1、(广东省广州执信中学、中山纪念中学、深圳外国语学校三校期末联考)设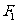 、
、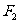 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点.
(Ⅰ)若P是该椭圆上的一个动点,求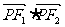 的最大值和最小值;
的最大值和最小值;
(Ⅱ)是否存在过点A(5,0)的直线l与椭圆交于不同的两点C、D,使得|F2C|=|F2D|?若存在,求直线l的方程;若不存在,请说明理由.
解:(Ⅰ)易知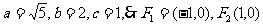
设P(x,y),则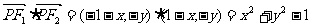

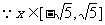 ,
,
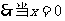 ,即点P为椭圆短轴端点时,
,即点P为椭圆短轴端点时,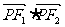 有最小值3;
有最小值3;
当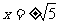 ,即点P为椭圆长轴端点时,
,即点P为椭圆长轴端点时,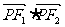 有最大值4
有最大值4
(Ⅱ)假设存在满足条件的直线l易知点A(5,0)在椭圆的外部,当直线l的斜率不存在时,直线l与椭圆无交点,所在直线l斜率存在,设为k
直线l的方程为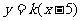
由方程组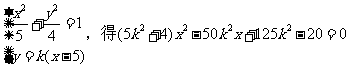
依题意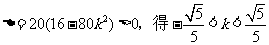
当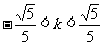 时,设交点C
时,设交点C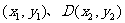 ,CD的中点为R
,CD的中点为R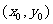 ,
,
则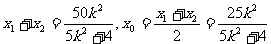
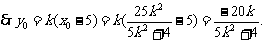
又|F2C|=|F2D|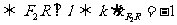
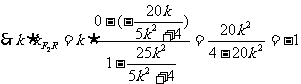
∴20k2=20k2-4,而20k2=20k2-4不成立, 所以不存在直线 ,使得|F2C|=|F2D|
,使得|F2C|=|F2D|
综上所述,不存在直线l,使得|F2C|=|F2D|
10.(2005天津)
已知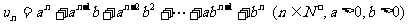

(Ⅰ)当 时,求数列
时,求数列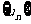 的前n项和
的前n项和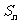
(Ⅱ)求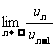 。
。
解:(Ⅰ)当 时,
时,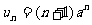 .这时数列
.这时数列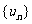 的前
的前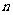 项和
项和
 . ①
. ①
①式两边同乘以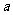 ,得
,得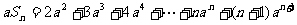 ②
②
①式减去②式,得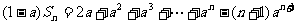
若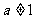 ,
,
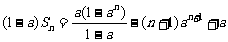 ,
,
若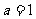 ,
,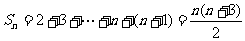
(Ⅱ)由(Ⅰ),当 时,
时,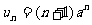 ,
,
则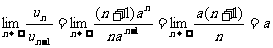 .
.
当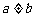 时,
时,
 此时,
此时,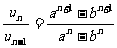 .
.
若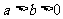 ,
,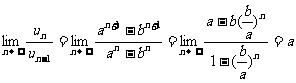 .
.
若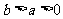 ,
,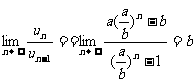 .
.
[探索题] 已知正项数列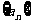 满足
满足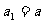 (
(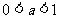 ),且
),且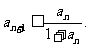
求证(1)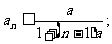 (2)
(2)
证明:(1)将条件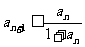 变形,得
变形,得
于是,有
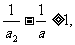
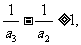
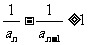
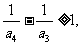 …………
…………
将这n-1个不等式叠加,得 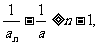
故 
(2)注意到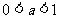 ,于是由(1)得
,于是由(1)得
 ,
,
从而,有 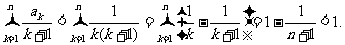
9. 数列{an}中,a1=8,a4=2,且满足an+2-2an+1+an=0(n∈N*).
(1)求数列{an}的通项公式.
(2)设bn= (n∈N*),Sn=b1+b2+…+bn,是否存在最大的整数m,使得任意的n均有Sn>
(n∈N*),Sn=b1+b2+…+bn,是否存在最大的整数m,使得任意的n均有Sn> 总成立?若存在,求出m;若不存在,请说明理由.
总成立?若存在,求出m;若不存在,请说明理由.
解:(1)∵an+2-2an+1+an=0,
∴an+2-an+1=an+1-an(n∈N*).
∴{an}是等差数列.设公差为d,
又a1=8,a4=a1+3d=8+3d=2,
∴d=-2.∴an=-2n+10.
(2)bn= =
=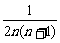
=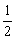 (
(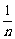 -
- ),
),
∴Sn=b1+b2+…+bn=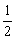 [(1-
[(1-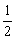 )+(
)+(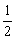 -
- )+…+(
)+…+(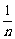 -
- )]
)]
=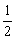 (1-
(1- )=
)=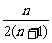 .
.
假设存在整数m满足Sn> 总成立.
总成立.
又Sn+1-Sn=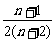 -
-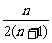
=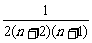 >0,
>0,
∴数列{Sn}是单调递增的.
∴S1=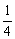 为Sn的最小值,故
为Sn的最小值,故 <
<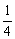 ,
,
即m<8.又m∈N*,
∴适合条件的m的最大值为7.
8.数列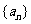 的前n项和为S
的前n项和为S ,且
,且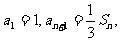 n=1,2,3….求
n=1,2,3….求
(I) 的值及数列
的值及数列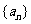 的通项公式;
的通项公式;
(II)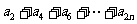 的值.
的值.
解:(I)由a1=1,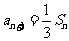 ,n=1,2,3,……,得
,n=1,2,3,……,得
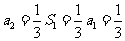 ,
,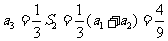 ,
,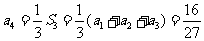 ,
,
由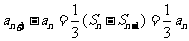 (n≥2),得
(n≥2),得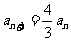 (n≥2),
(n≥2),
又a2=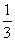 ,所以an=
,所以an=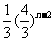 (n≥2),
(n≥2),
∴ 数列{an}的通项公式为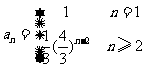 ;
;
(II)由(I)可知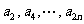 是首项为
是首项为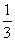 ,公比为
,公比为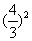 项数为n的等比数列,∴
项数为n的等比数列,∴ 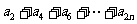 =
=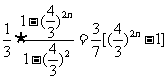
7. 设数列{an}的首项a1=a≠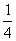 ,且
,且 ,
,
记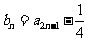 ,n==l,2,3,…·.
,n==l,2,3,…·.
(I)求a2,a3;
(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)求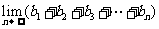 .
.
解:(I)a2=a1+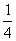 =a+
=a+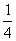 ,a3=
,a3=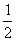 a2=
a2=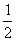 a+
a+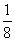 ;
;
(II)∵ a4=a3+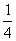 =
=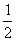 a+
a+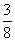 , 所以a5=
, 所以a5=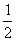 a4=
a4=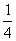 a+
a+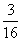 ,
,
所以b1=a1-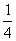 =a-
=a-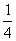 , b2=a3-
, b2=a3-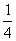 =
=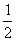 (a-
(a-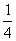 ), b3=a5-
), b3=a5-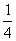 =
=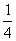 (a-
(a-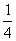 ),
),
猜想:{bn}是公比为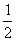 的等比数列·
的等比数列·
证明如下:
因为bn+1=a2n+1-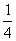 =
=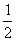 a2n-
a2n-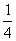 =
=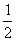 (a2n-1-
(a2n-1-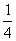 )=
)=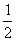 bn, (n∈N*)
bn, (n∈N*)
所以{bn}是首项为a-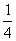 , 公比为
, 公比为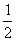 的等比数列·
的等比数列·
(III)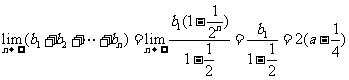 .
.
5.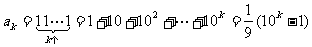
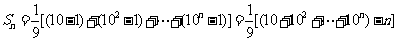
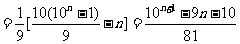 ;6. 解:因为
;6. 解:因为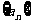 为等比数列,所以
为等比数列,所以
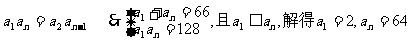
依题意知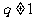
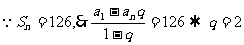

[解答题]
4.an=sn-sn-1=(a+b-bn)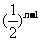
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com