
14、(北京市海淀区2008年高三统一练习一)已知点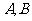 分别是射线
分别是射线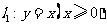 ,
,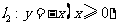 上的动点,
上的动点, 为坐标原点,且
为坐标原点,且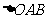 的面积为定值2.
的面积为定值2.
(I)求线段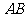 中点
中点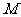 的轨迹
的轨迹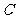 的方程;
的方程;
(II)过点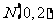 作直线
作直线 ,与曲线
,与曲线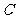 交于不同的两点
交于不同的两点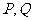 ,与射线
,与射线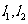 分别交于点
分别交于点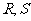 ,若点
,若点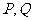 恰为线段
恰为线段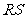 的两个三等分点,求此时直线
的两个三等分点,求此时直线 的方程.
的方程.
解:(I)由题可设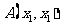 ,
,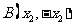 ,
,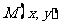 ,其中
,其中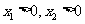 .
.
则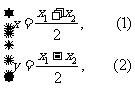 1分
1分
∵ 的面积为定值2,
的面积为定值2,
∴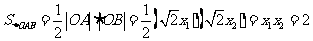 .
2分
.
2分
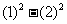 ,消去
,消去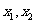 ,得:
,得: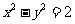 .
4分
.
4分
由于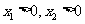 ,∴
,∴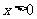 ,所以点
,所以点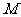 的轨迹方程为
的轨迹方程为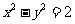 (x>0).
(x>0).
5分
(II)依题意,直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为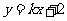 .
.
由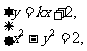 消去
消去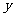 得:
得: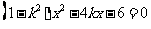 ,
6分
,
6分
设点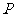 、
、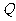 、
、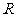 、
、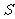 的横坐标分别是
的横坐标分别是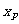 、
、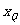 、
、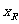 、
、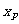 ,
,
∴由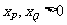 得
得 8分
8分
解之得: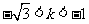 .
.
∴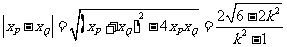 .
9分
.
9分
由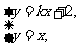 消去
消去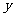 得:
得: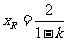 ,
,
由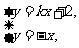 消去
消去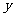 得:
得: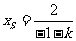 ,
,
∴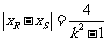 .
10分
.
10分
由于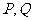 为
为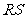 的三等分点,∴
的三等分点,∴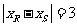
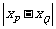 .
11分
.
11分
解之得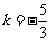 .
12分
.
12分
 经检验,此时
经检验,此时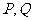 恰为
恰为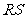 的三等分点,故所求直线方程为
的三等分点,故所求直线方程为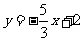 .
.
12、(北京市东城区2008年高三综合练习二)已知双曲线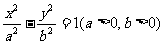 的一条渐近线方程为
的一条渐近线方程为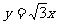 ,两条准线的距离为l.
,两条准线的距离为l.
(1)求双曲线的方程;
(2)直线l过坐标原点O且和双曲线交于两点M、N,点P为双曲线上异于M、N的一点,且直线PM,PN的斜率均存在,求kPM·kPN的值.
(1)解:依题意有:
可得双曲线方程为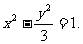 ………………………………………………6分
………………………………………………6分
(2)解:设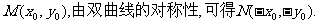
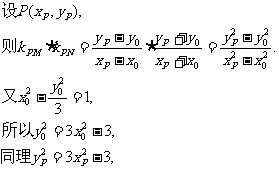
所以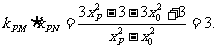
11、(北京市东城区2008年高三综合练习一)已知定圆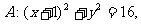 圆心为A,动圆M过点B(1,0)且和圆A相切,动圆的圆心M的轨迹记为C.
圆心为A,动圆M过点B(1,0)且和圆A相切,动圆的圆心M的轨迹记为C.
(I)求曲线C的方程;
(II)若点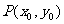 为曲线C上一点,求证:直线
为曲线C上一点,求证:直线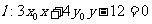 与曲线C有且只有一个交点.
与曲线C有且只有一个交点.
解:(I)圆A的圆心为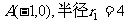 ,
,
设动圆M的圆心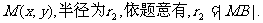
由|AB|=2,可知点B在圆A内,从而圆M内切于圆A,
故|MA|=r1-r2,即|MA|+|MB|=4,
所以,点M的轨迹是以A,B为焦点的椭圆,
设椭圆方程为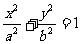 ,由
,由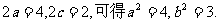
故曲线C的方程为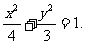 …………6分
…………6分
(II)当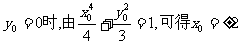 ,
,

消去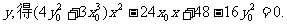 ①
①
由点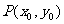 为曲线C上一点,
为曲线C上一点,

于是方程①可以化简为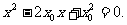 解得
解得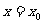 ,
,

综上,直线l与曲线C有且只有一个交点,且交点为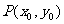 .
.
10、(北京市崇文区2008年高三统一练习一)已知抛物线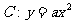 ,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
,点P(1,-1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
(I)求抛物线C的焦点坐标;
(II)若点M满足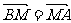 ,求点M的轨迹方程.
,求点M的轨迹方程.
解:(I)将P(1,-1)代入抛物线C的方程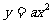 得a=-1,
得a=-1,
∴抛物线C的方程为 ,即
,即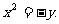
焦点坐标为F(0,-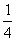 ).……………………………………4分
).……………………………………4分
(II)设直线PA的方程为 ,
,
联立方程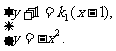 消去y得
消去y得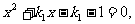
则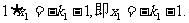
由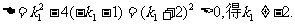 ………………7分
………………7分
同理直线PB的方程为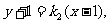
联立方程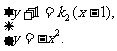 消去y得
消去y得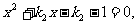
则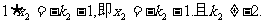
又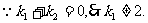 …………………………9分
…………………………9分
设点M的坐标为(x,y),由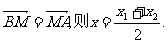
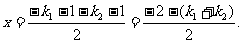
又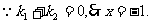 …………………………………………11分
…………………………………………11分
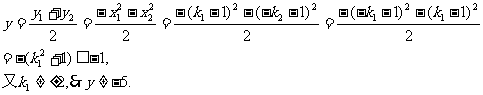
∴所求M的轨迹方程为:
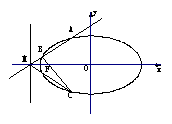
9、(北京市朝阳区2008年高三数学一模)已知椭圆W的中心在原点,焦点在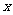 轴上,离心率为
轴上,离心率为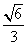 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为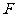 ,过左准线与
,过左准线与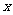 轴的交点
轴的交点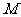 任作一条斜率不为零的直线
任作一条斜率不为零的直线 与椭圆W交于不同的两点
与椭圆W交于不同的两点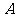 、
、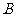 ,点
,点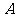 关于
关于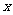 轴的对称点为
轴的对称点为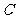 .
.
(Ⅰ)求椭圆W的方程;
(Ⅱ)求证: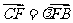 (
(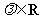 );
);
(Ⅲ)求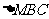 面积
面积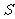 的最大值.
的最大值.
解:(Ⅰ)设椭圆W的方程为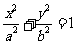 ,由题意可知
,由题意可知
 解得
解得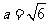 ,
,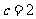 ,
,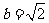 ,
,
所以椭圆W的方程为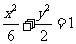 .……………………………………………4分
.……………………………………………4分
(Ⅱ)解法1:因为左准线方程为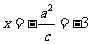 ,所以点
,所以点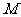 坐标为
坐标为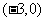 .于是可设直线
.于是可设直线 的方程为
的方程为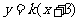 .
.
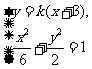 得
得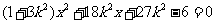 .
.
由直线 与椭圆W交于
与椭圆W交于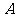 、
、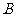 两点,可知
两点,可知
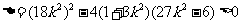 ,解得
,解得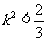 .
.
设点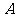 ,
,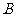 的坐标分别为
的坐标分别为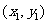 ,
,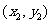 ,
,
则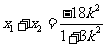 ,
,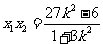 ,
,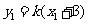 ,
,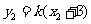 .
.
因为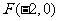 ,
,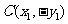 ,
,
所以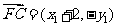 ,
,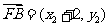 .
.
又因为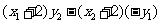
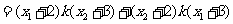
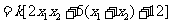
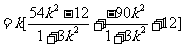
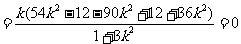 ,
,
所以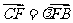 . ……………………………………………………………10分
. ……………………………………………………………10分
解法2:因为左准线方程为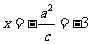 ,所以点
,所以点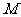 坐标为
坐标为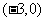 .
.
于是可设直线 的方程为
的方程为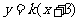 ,点
,点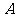 ,
,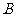 的坐标分别为
的坐标分别为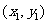 ,
,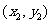 ,
,
则点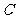 的坐标为
的坐标为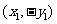 ,
,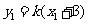 ,
,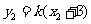 .
.
由椭圆的第二定义可得
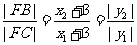 ,
,
所以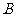 ,
,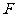 ,
,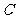 三点共线,即
三点共线,即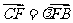 .…………………………………10分
.…………………………………10分
(Ⅲ)由题意知
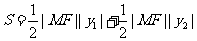
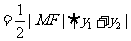
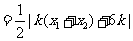
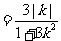
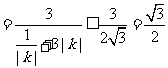 ,
,
当且仅当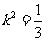 时“=”成立,
时“=”成立,
所以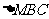 面积
面积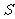 的最大值为.
的最大值为.
8、(安徽省巢湖市2008届高三第二次教学质量检测)已知点R(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上 ,且满足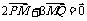 ,
,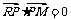 .
.
(Ⅰ)⑴当点P在y轴上移动时,求点M的轨迹C的方程;
(Ⅱ)设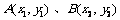 为轨迹C上两点,且
为轨迹C上两点,且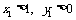 ,N(1,0),求实数
,N(1,0),求实数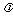 ,使
,使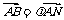 ,且
,且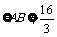 .
.
解:(Ⅰ)设点M(x,y),由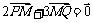 得P(0,
得P(0,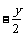 ),Q(
),Q(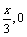 ).
).
由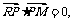 得(3,
得(3,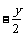 )·(
)·(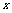 ,
,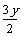 )=0,即
)=0,即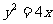
又点Q在x轴的正半轴上,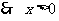 故点M的轨迹C的方程是
故点M的轨迹C的方程是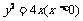 .……6分
.……6分
(Ⅱ)解法一:由题意可知N为抛物线C:y2=4x的焦点,且A、B为过焦点N的直线与抛物线C的两个交点。
当直线AB斜率不存在时,得A(1,2),B(1,-2),|AB|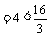 ,不合题意;………7分
,不合题意;………7分
当直线AB斜率存在且不为0时,设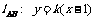 ,代入
,代入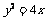 得
得
则|AB|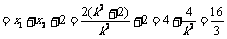 ,解得
,解得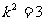 …………………10分
…………………10分
代入原方程得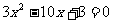 ,由于
,由于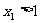 ,所以
,所以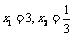 ,
,
由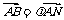 ,得
,得  .
……………………13分
.
……………………13分
解法二:由题设条件得


由(6)、(7)解得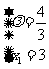 或
或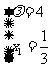 ,又
,又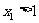 ,故
,故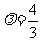 .
.
7、(安徽省淮南市2008届高三第一次模拟考试)已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线y=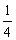 x2的焦点,离心率等于
x2的焦点,离心率等于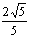 .
.
(1)求椭圆C的方程;
(2)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若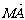 =λ1
=λ1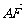 ,
,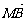 =λ2
=λ2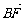 ,求证λ1+λ2为定值.
,求证λ1+λ2为定值.
解:(I)设椭圆C的方程为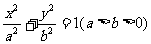 ,则由题意知b = 1.
,则由题意知b = 1.
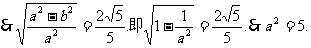
∴椭圆C的方程为
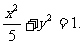 …………………………………………………5分
…………………………………………………5分
(II)方法一:设A、B、M点的坐标分别为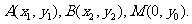
易知F点的坐标为(2,0).

将A点坐标代入到椭圆方程中,得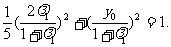
去分母整理得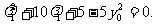 …………………………………………10分
…………………………………………10分

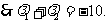 …………………………………………………………12分
…………………………………………………………12分
方法二:设A、B、M点的坐标分别为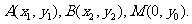 又易知F点的坐标为(2,0).
又易知F点的坐标为(2,0).
显然直线l存在的斜率,设直线l的斜率为k,则直线l的方程是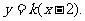
将直线l的方程代入到椭圆C的方程中,消去y并整理得
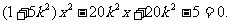 ……………………………………7分
……………………………………7分
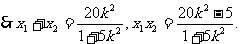 ……………………………………8分
……………………………………8分
又
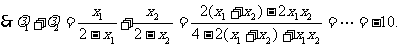
6、(江西省五校2008届高三开学联考)已知圆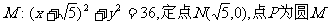 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足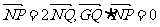 .
.
(I)求点G的轨迹C的方程;
(II)过点(2,0)作直线 ,与曲线C交于A、B两点,O是坐标原点,设
,与曲线C交于A、B两点,O是坐标原点,设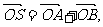 是否存在这样的直线
是否存在这样的直线 ,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线
,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
解:(1)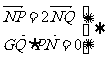 Q为PN的中点且GQ⊥PN
Q为PN的中点且GQ⊥PN
 GQ为PN的中垂线
GQ为PN的中垂线 |PG|=|GN|
|PG|=|GN|
∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长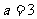 ,半焦距
,半焦距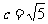 ,∴短半轴长b=2,∴点G的轨迹方程是
,∴短半轴长b=2,∴点G的轨迹方程是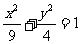 ………5分
………5分
(2)因为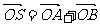 ,所以四边形OASB为平行四边形
,所以四边形OASB为平行四边形
若存在l使得|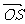 |=|
|=|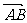 |,则四边形OASB为矩形
|,则四边形OASB为矩形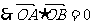
若l的斜率不存在,直线l的方程为x=2,由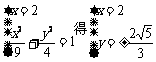
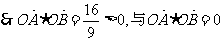 矛盾,故l的斜率存在. ………7分
矛盾,故l的斜率存在. ………7分
设l的方程为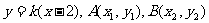
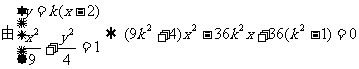
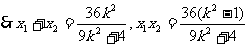 ①
①
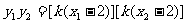
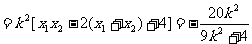 ② ……………9分
② ……………9分
把①、②代入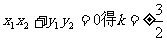
∴存在直线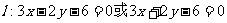 使得四边形OASB的对角线相等.
使得四边形OASB的对角线相等.
5、(安徽省皖南八校2008届高三第一次联考)已知线段AB过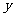 轴上一点
轴上一点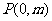 ,斜率为
,斜率为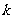 ,两端点A,B到
,两端点A,B到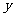 轴距离之差为
轴距离之差为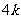
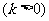 ,
,
(1)求以O为顶点,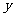 轴为对称轴,且过A,B两点的抛物线方程;
轴为对称轴,且过A,B两点的抛物线方程;
(2)设Q为抛物线准线上任意一点,过Q作抛物线的两条切线,切点分别为M,N,求证:直线MN过一定点;
解:(1)设抛物线方程为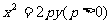 ,AB的方程为
,AB的方程为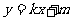 ,
,
联立消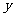 整理,得
整理,得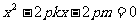 ;∴
;∴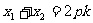 ,
,
又依题有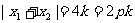 ,∴
,∴ ,∴抛物线方程为
,∴抛物线方程为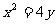 ;
;
(2)设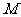
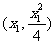 ,
,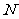
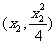 ,
,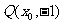 ,∵
,∵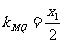 ,
,
∴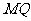 的方程为
的方程为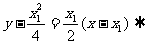
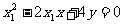 ;
;
∵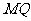 过
过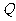 ,∴
,∴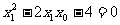 ,同理
,同理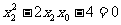
∴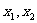 为方程
为方程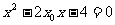 的两个根;∴
的两个根;∴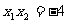 ;
;
又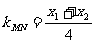 ,∴
,∴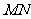 的方程为
的方程为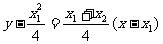
∴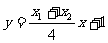 ,显然直线
,显然直线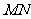 过点
过点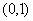
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com