
1. 设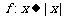 是集合A到集合B的映射,且集合B中的每一个元素都有原象,若
是集合A到集合B的映射,且集合B中的每一个元素都有原象,若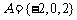 ,则
,则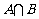 等于(C)
等于(C)
A.{0} B.{2} C.{0,2} D.{-2,0}
解析:B={0,2},∴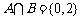
21.解:(1) 由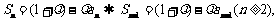
相减得: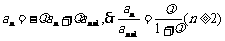 ,
,
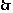 数列
数列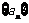 是等比数列。
是等比数列。
(2)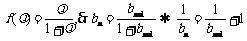 ,
,
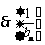 是首项为
是首项为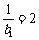 ,公差为1的等差数列;
,公差为1的等差数列;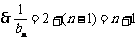 ,
,
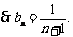
(3)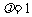 时,
时,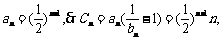
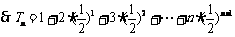 ,
①
,
①
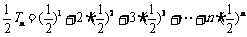 ②
②
①-②得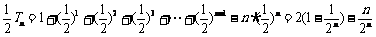 ,
,
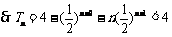 ,
,
又因为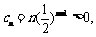
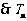 单调递增,
单调递增,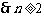 时
时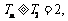
故当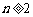 时,
时,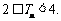
21.(本小题满分14分)设数列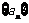 的前
的前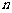 项和为
项和为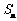 ,且
,且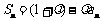 ,其中
,其中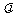 为常数,且
为常数,且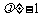 、0.
、0.
(1)证明:数列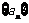 是等比数列;
是等比数列;
(2)设数列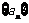 的公比
的公比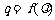 ,数列
,数列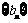 满足
满足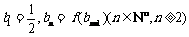 ,求数列
,求数列
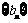 的通项公式;
的通项公式;
(3)设 ,数列
,数列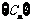 的前
的前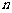 项和为
项和为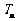 ,求证:当
,求证:当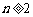 时,
时,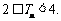
20.解析:(1)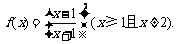
∵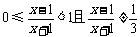 ,∴函数
,∴函数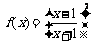 的值域为
的值域为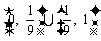
由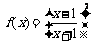 ,得
,得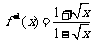 ,因此,函数
,因此,函数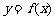 的反函数
的反函数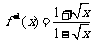
(2)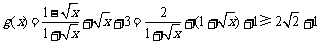 ,当且仅当
,当且仅当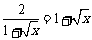 ,
,
即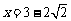 时,
时,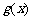 有最小值
有最小值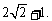
(3)由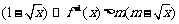 ,得
,得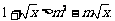
设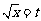 ,则
,则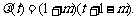
根据题意,对区间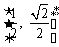 中的一切t值,
中的一切t值,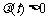 恒成立.
恒成立.
则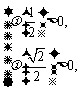 得
得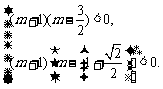 ∴
∴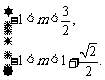
∴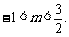 即实数m的取值范围是
即实数m的取值范围是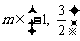
20.(本小题满分13分)已知函数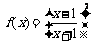 (其中x≥1且x≠2).
(其中x≥1且x≠2).
(1)求函数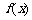 的反函数
的反函数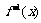 ;
;
(2)设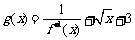 ,求函数
,求函数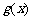 最小值及相应的x值;
最小值及相应的x值;
(3)若不等式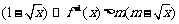 对于区间
对于区间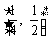 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.
19.解析:(1)由题知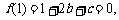
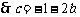
记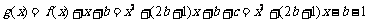 ,
,
则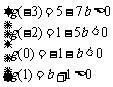
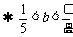 ,
即
,
即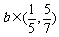 .
.
(2)令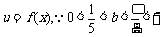 ,
,
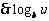 在区间
在区间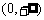 上是减函数.
上是减函数.
而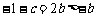 ,函数
,函数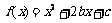 的对称轴为
的对称轴为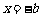 ,
,
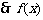 在区间
在区间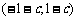 上单调递增.
上单调递增.
从而函数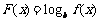 在区间
在区间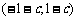 上为减函数.
上为减函数.
且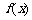 在区间
在区间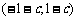 上恒有
上恒有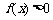 ,只需要
,只需要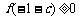 ,
,
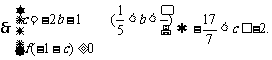
19.(本小题满分12分)已知二次函数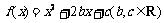 满足
满足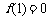 ,且关于
,且关于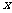 的方程
的方程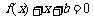 的两个实数根分别在区间
的两个实数根分别在区间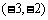 、
、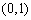 内.
内.
(1)求实数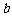 的取值范围;
的取值范围;
(2)若函数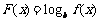 在区间
在区间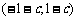 上具有单调性,求实数
上具有单调性,求实数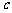 的取值范围.
的取值范围.
18.解:(1)设前n个月投资总额为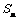 ,
,
则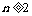 时,
时,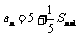 ,∴
,∴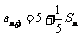 ,
,
两式相减得: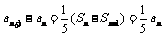 ,∴
,∴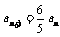 ,
,
又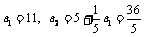 ,∴
,∴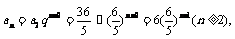
又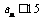 ,∴
,∴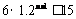 ,∴
,∴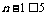 ,∴
,∴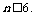
∴
(2)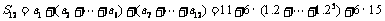
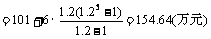
故预计2010年全年共需投资154.64万元.
18.(本题满分12分)某企业为了适应市场需求,计划从2010年元月起,在每月固定投资5万元的基础上,元月份追加投资6万元,以后每月的追加投资额均为之前几个月投资额总和的20%,但每月追加部分最高限额为10万元. 记第n个月的投资额为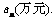
(1)求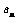 与n的关系式;
与n的关系式;
(2)预计2010年全年共需投资多少万元?(精确到0.01,参考数据: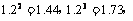
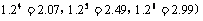
17.解:(1)由题设知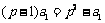 ,解得
,解得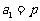 。
。
由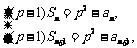 两式作差得
两式作差得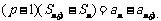
所以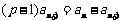 ,即
,即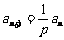 ,
,
可见,数列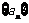 是首项为
是首项为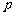 ,公比为
,公比为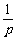 的等比数列。
的等比数列。
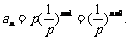
(2)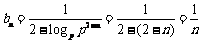 .
.
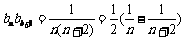
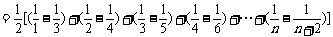
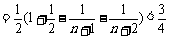 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com