
10.(2008年上海理5)若向量(a、(b满足|(a|=1,|(b|=2,且(a与(b的夹角为,则|(a+(b|= .
[答案]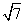 [解析]
[解析]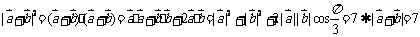 .
.
9.(2008年江苏5)已知向量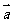 和
和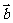 的夹角为
的夹角为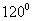 ,
,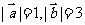 ,则
,则 .
.
[解析]本小题考查向量的线性运算.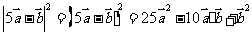
=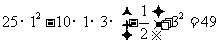 ,
, 7
7
8.(2008年海南理13)已知向量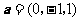 ,
,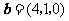 ,
,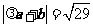 且
且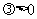 ,
,
则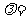 .
.
解:由题意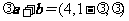
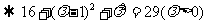
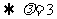
7.(2009年安徽理14)给定两个长度为1的平面向量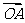 和
和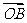 ,它们的夹角为
,它们的夹角为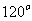 .
.
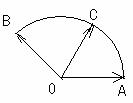 如图所示,点C在以O为圆心的圆弧
如图所示,点C在以O为圆心的圆弧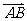 上变动.
上变动.
若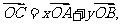 其中
其中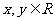 ,则
,则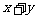
的最大值是________.
[解析]设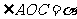
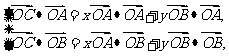 ,即
,即
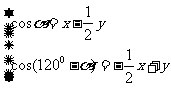
∴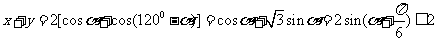
6.(2009年天津理15)在四边形ABCD中,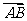 =
=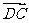 =(1,1),
=(1,1),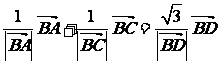 ,则四边形ABCD的面积是
,则四边形ABCD的面积是
[考点定位]本小题考查向量的几何运算,基础题。
解析:由题知四边形ABCD是菱形,其边长为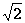 ,且对角线BD等于边长的
,且对角线BD等于边长的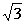 倍,所以
倍,所以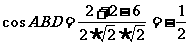 ,故
,故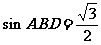 ,
,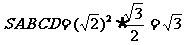
5.(2009年广东理10) 若平面向量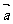 ,
,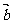 满足
满足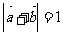 ,
,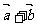 平行于
平行于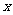 轴,
轴,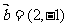 ,则
,则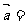
[解析]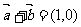 或
或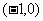 ,则
,则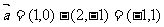
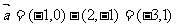 .
.
4.(209年江苏2)已知向量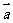 和向量
和向量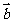 的夹角为
的夹角为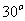 ,
,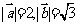 ,则向量
,则向量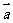 和向量
和向量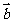 的数量积
的数量积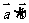 = 。
= 。
[解析] 考查数量积的运算。 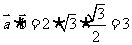
3. (2010年广东理10)若向量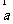 =(1,1,x),
=(1,1,x), 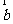 =(1,2,1),
=(1,2,1), 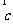 =(1,1,1),满足条件
=(1,1,1),满足条件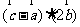 =-2,则
=-2,则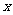 = .
= .
[答案]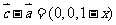 ,
,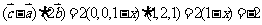 ,解得
,解得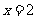 .
.
2.(2010年浙江理16)已知平面向量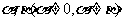 满足
满足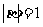 ,且
,且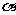 与
与 的夹角为120°,则
的夹角为120°,则 的取值范围是__________________ .
的取值范围是__________________ .
解析:利用题设条件及其几何意义表示在三角形中,即可迎刃而解,本题主要考察了平面向量的四则运算及其几何意义,突出考察了对问题的转化能力和数形结合的能力,属中档题。
1.( 2010年陕西理11) 已知向量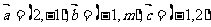 ,若
,若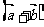 ∥
∥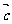 ,则
,则 .
.
[答案]-1[解析]∵
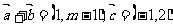 ,∴由
,∴由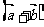 ∥
∥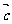 得
得 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com