
3.若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m,则m的范围是
A.(1,2) B.(2,+∞) C.[3,+∞ D.(3,+∞)
D.(3,+∞)
4已知等差数列{an}中,|a3|=|a9|,公差d<0,则使前n项和Sn取最大值的正整数n是
A、4或5 B、5或6 C、6或7 D、8或9
1.已知等差数列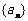 中,
中,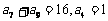 ,则
,则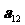 的值是
的值是
A.15 B.30 C.31 D.64
2设m∈N+,log2m的整数部分用F(m)表示,则F(1)+F(2)+…+F(1024)的值是
A、 8204 B、8192 C、9218 D、8021
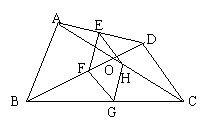
28、如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别
是AD,BD, BC,AC的中点。
(1)求证:四边形EFGH是平行四边形;(4分)
(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?
并证明你的结论。(6分)
27.小颖准备到甲、乙两个商场去应聘.如图,l1、l2分别表示了甲、乙两商场每月付给员工工资y1、y2(元)与销售商品的件数x(件)的关系.
(1)根据图象分别求出y1、y2与x的函数关系式;(6分)
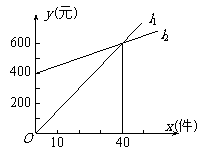 (2)根据图象直接回答:如果小颖决定应聘,她可能选择甲商场还是乙商场?(3分)
(2)根据图象直接回答:如果小颖决定应聘,她可能选择甲商场还是乙商场?(3分)
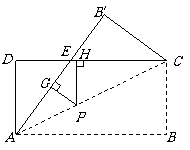
26.如图,将矩形纸片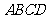 沿其对角线
沿其对角线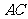 折叠,使点
折叠,使点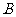 落到点
落到点 的位置,
的位置,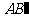 与
与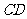 交于点
交于点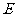 .
.
(1)试找出一个与 全等的三角形,并加以证明;(5分)
全等的三角形,并加以证明;(5分)
 (2)若
(2)若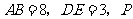 为线段
为线段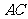 上任意一点,
上任意一点,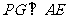 于
于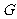 ,
,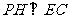 于
于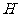 .试求
.试求 的值,并说明理由.(4分)
的值,并说明理由.(4分)
25.如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.
(1)求证:BE=DG;(5分)
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,说出旋转
过程;若不存在,请说明理由.(3分)
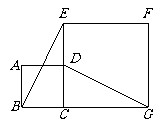
24.四边形ABCD是正方形.
(1)如图1,点G是BC边上任意一点(不与B、C两点重合),连接AG,
作BF⊥AG于点F,DE⊥AG于点E.求证:△ABF≌△DAE;(5分)
(2)在(1)中,线段EF与AF、BF的等量关系是 (直接写出
结论即可,不需要证明);(2分)
(3)如图2,点G是CD边上任意一点(不与C、D两点重合),连接AG,
作BF⊥AG于点F,DE⊥AG于点E.那么图中全等三角形是 ,
线段EF与AF、BF的等量关系是 (直接写出结论即可,
不需要证明).(5分)


23.(10分)为了解某中学九年级学生中考体育成绩情况,现从中抽取部分
学生的体育成绩进行分段(A:50分、B:49-40分、C:39-30分、
D:29-0分)统计结果如图1、图2所示.

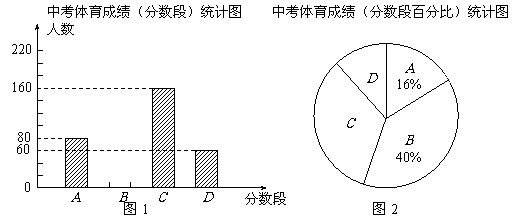

根据上面提供的信息,回答下列问题:
(1)本次抽查了多少名学生的体育成绩?(2分)
(2)在图1中,将选项B的部分补充完整?(3分)
(3)求图2中D部分所占的比例;(2分)
(4)已知该校九年级共有900名学生,请估计该校九年级学生体育成绩达到40
分以上(含40分)的人数.(3分)
22.(本小题8分)如图,平行四边形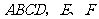 两点在对角线
两点在对角线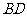 上,
上,
且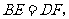 连结
连结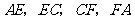 求证:四边形
求证:四边形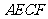 是平行四边形.
是平行四边形.

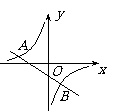
21.(10分)如图,反比例函数y=(m≠0)与一次函数y=kx+b(k≠0)的图象相交于A、B两点,点A的坐标为(-6,2),点B的坐标为(3,n).求反比例函数和一次函数的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com