
17. 解:(1)依题可设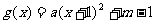 (
(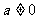 ),则
),则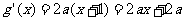 ;
;
又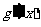 的图像与直线
的图像与直线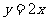 平行
平行 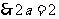
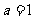
 ,
, 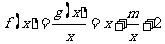 ,
,
设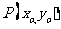 ,则
,则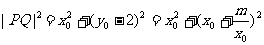


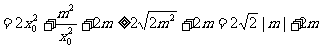
当且仅当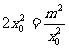 时,
时,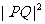 取得最小值,即
取得最小值,即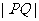 取得最小值
取得最小值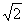
当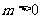 时,
时,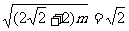 解得
解得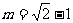
当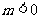 时,
时,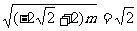 解得
解得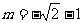
(2)由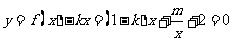 (
(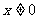 ),得
),得
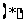
当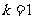 时,方程
时,方程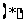 有一解
有一解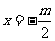 ,函数
,函数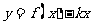 有一零点
有一零点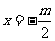 ;
;
当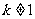 时,方程
时,方程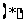 有二解
有二解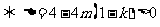 ,
,
若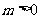 ,
,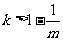 ,
,
函数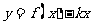 有两个零点
有两个零点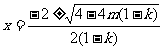 ,即
,即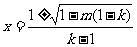 ;
;
若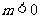 ,
,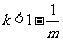 ,
,
函数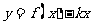 有两个零点
有两个零点 ,即
,即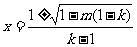 ;
;
当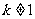 时,方程
时,方程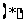 有一解
有一解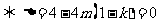 ,
, 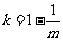 ,
,
函数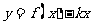 有一零点
有一零点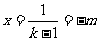
综上,当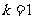 时, 函数
时, 函数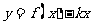 有一零点
有一零点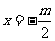 ;
;
当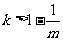 (
(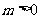 ),或
),或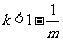 (
(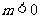 )时,
)时,
函数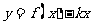 有两个零点
有两个零点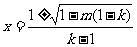 ;
;
当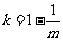 时,函数
时,函数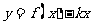 有一零点
有一零点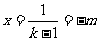 .
.
15. 解:(Ⅰ)由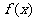 的图象经过P(0,2),知d=2,所以
的图象经过P(0,2),知d=2,所以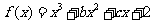 .
.
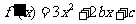 由于函数
由于函数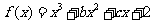 在点
在点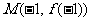 处的切线方程是
处的切线方程是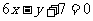 ,∴
,∴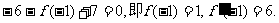

故所求函数的解析式是  .
.
(Ⅱ)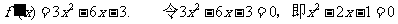 .
.
解得 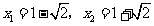 .当
.当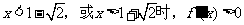 ;
;
当 .
.
故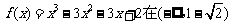 内是增函数,在
内是增函数,在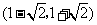 内是减函数,
内是减函数,
在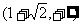 内是增函数.
内是增函数.
17. (2009广东卷理)(本小题满分10分)已知二次函数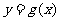 的导函数的图像与直线
的导函数的图像与直线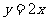 平行,且
平行,且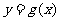 在
在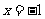 处取得极小值
处取得极小值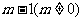 .设
.设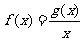 .
.
(1)若曲线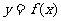 上的点
上的点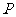 到点
到点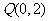 的距离的最小值为
的距离的最小值为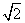 ,求
,求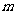 的值;
的值;
(2)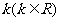 如何取值时,函数
如何取值时,函数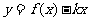 存在零点,并求出零点.
存在零点,并求出零点.
新安中学高三数学单元测试题---函数与导数答案
16.(本题满分10分)统计表明,某种型号的汽车在匀速行驶中每小时的耗油量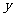 (升)关于行驶速度
(升)关于行驶速度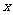 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: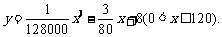
已知甲、乙两地相距100千米。
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
15. (本题满分10分)已知函数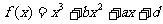 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M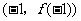 处的切线方程为
处的切线方程为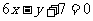 .
.
(Ⅰ)求函数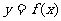 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数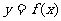 的单调区间.
的单调区间.
14.已知函数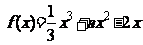 在区间
在区间
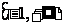 上有极大值和极小值,则实数
上有极大值和极小值,则实数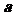 的取值范围是
。
的取值范围是
。
13.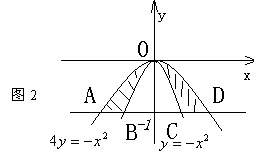 如图2,由两条曲线
如图2,由两条曲线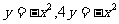 及直线
及直线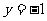
所围成的图形的面积为
12.已知函数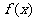 是定义在R上的奇函数,
是定义在R上的奇函数,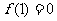 ,
,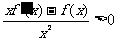
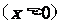 ,则不等式
,则不等式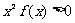 的解集是
的解集是 
11.函数f(x)=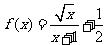 的最大值为
的最大值为
10.若函数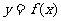 的定义域是
的定义域是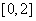 ,则函数
,则函数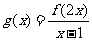 的定义域是
的定义域是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com