
(二)填空题:
7、(07重庆)设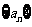 为公比
为公比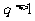 的等比数列,若
的等比数列,若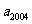 和
和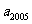 是方程
是方程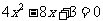 的两根,则
的两根,则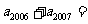 ______;
______;
8、(06重庆)在数列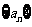 中,若
中,若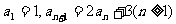 ,则该数列的通项
,则该数列的通项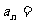 _________。
_________。
(一)选择题:
1、(07重庆)若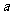 是
是 与
与 的等比中项,则
的等比中项,则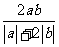 的最大值为( )
的最大值为( )
A、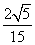 B、
B、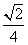 C、
C、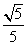 D、
D、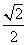
2、(07陕西)各项均为正数的等比数列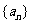 的前
的前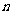 项和为
项和为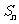 为,若
为,若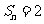 ,
,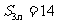 ,则
,则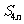 等于( )
等于( )
A、80 B、30 C、26 D、16
3、(06湖北)若互不相等的实数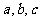 成等差数列,
成等差数列,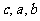 成等比数列,且
成等比数列,且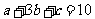 ,则
,则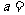 ( ) A、4 B、2 C、-2 D、-4
( ) A、4 B、2 C、-2 D、-4
4、(06湖南)若数列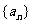 满足:
满足: 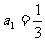 , 且对任意正整数
, 且对任意正整数 都有
都有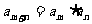 , 则
, 则
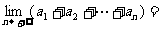 ( )
( )
A、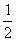 B、
B、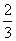 C、
C、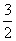 D、
D、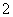
5、(06辽宁)在等比数列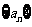 中,
中,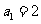 ,前
,前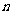 项和为
项和为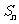 ,若数列
,若数列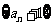 也是等比数列,则
也是等比数列,则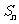 等于( ) A、
等于( ) A、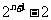 B、
B、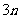 C、
C、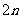 D、
D、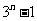
6、(05江苏)在各项都为正数的等比数列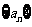 中,首项
中,首项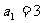 ,前三项和为21,则
,前三项和为21,则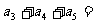 ( )
( )
A、33 B、72 C、84 D、189
例1、(06天津)已知数列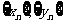 满足
满足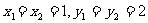 ,并且
,并且
 (
(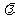 为非零参数,
为非零参数,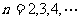 )。
)。
(1)若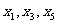 成等比数列,求参数
成等比数列,求参数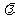 的值;(2)当
的值;(2)当 时,证明
时,证明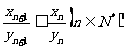 ;
;
(3)当 时,证明
时,证明 。
。
解:(I)由已知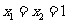 ,
,
且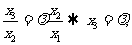
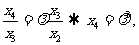
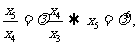
若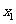 、
、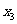 、
、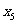 成等比数列,则
成等比数列,则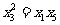 ,即
,即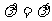 。
。
而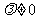 , 解得
, 解得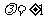 。
。
(II)由已知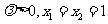 及
及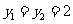 ,可得
,可得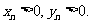
由不等式的性质,有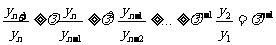
另一方面,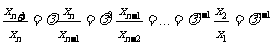
因此,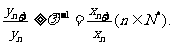 故
故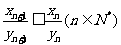
(III)当 时,由(II)可知
时,由(II)可知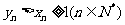
又由(II)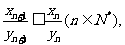 则
则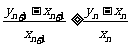
从而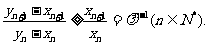 因此
因此
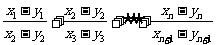
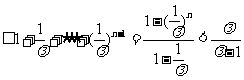

例2、(05全国Ⅱ18)已知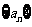 是各项均为正数的等差数列,
是各项均为正数的等差数列,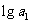 、
、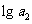 、
、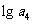 成等差数列.又
成等差数列.又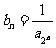 ,
,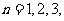 ….(Ⅰ)证明
….(Ⅰ)证明 为等比数列;(Ⅱ)如果无穷等比数列
为等比数列;(Ⅱ)如果无穷等比数列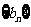 各项的和
各项的和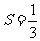 ,求数列
,求数列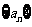 的首项
的首项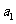 和公差
和公差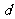 。
。
例3、(04吉林)数列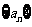 的前
的前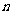 项和记为
项和记为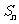 ,已知
,已知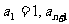 =
=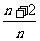
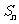 (
(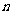 =1,2,3,…).证明:(Ⅰ)数列{
=1,2,3,…).证明:(Ⅰ)数列{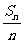 }是等比数列;(Ⅱ)
}是等比数列;(Ⅱ)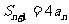 .
.
(三)解答题:
9、(07福建21)等差数列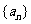 的前
的前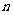 项和为
项和为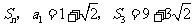 .
.
(Ⅰ)求数列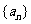 的通项
的通项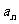 与前
与前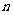 项和
项和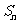 ;
;
(Ⅱ)设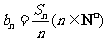 ,求证:数列
,求证:数列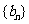 中任意不同的三项都不可能成为等比数列。
中任意不同的三项都不可能成为等比数列。
解:(Ⅰ)由已知得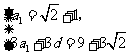 ,
,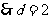 ,
,
故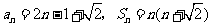 .
.
(Ⅱ)由(Ⅰ)得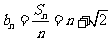 .
.
假设数列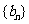 中存在三项
中存在三项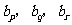 (
(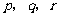 互不相等)成等比数列,则
互不相等)成等比数列,则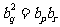 .
.
即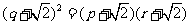 .
.
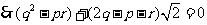
 ,
,
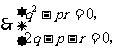
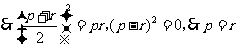 .
.
与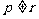 矛盾.
矛盾.
所以数列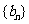 中任意不同的三项都不可能成等比数列.
中任意不同的三项都不可能成等比数列.
(二)填空题:
8、(06浙江)设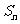 为等差数列
为等差数列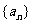 的前
的前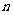 项和,若
项和,若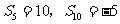 ,则公差为 (用数字作答)。
,则公差为 (用数字作答)。
(一)选择题:
1、(04全国)已知方程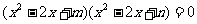 的四个根组成一个首项为
的四个根组成一个首项为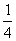 等差数列,则
等差数列,则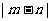 等于( )
等于( )
A、1
B、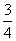 C、
C、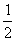 D、
D、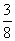
2、(04全国Ⅲ)设数列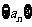 是等差数列,
是等差数列,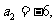
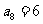 ,
,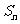 是数列
是数列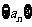 的前n项和,则( )
的前n项和,则( )
A、S4<S5 B、S4=S5 C、S6<S5 D、S6=S5
3、(05福建)
4、(06全国Ⅰ10)设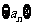 是公差为正数的等差数列,若
是公差为正数的等差数列,若 ,
,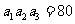 ,则
,则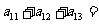 ( )
( )
A、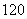 B、
B、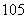 C、
C、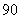 D、
D、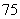
5、(06全国Ⅱ11)设Sn是等差数列{an}的前n项和,若=,则=( )
A、 B、 C、 D、
6、(06天津)已知数列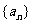

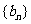 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为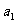

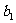 ,且
,且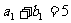 ,
,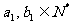 .设
.设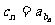 (
(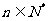 ),则数列
),则数列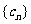 的前10项和等于( )
的前10项和等于( )
A、55 B、70 C、85 D、100
7、(06重庆)在等差数列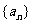 中,若
中,若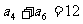 ,
,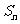 是数列
是数列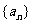 的前
的前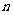 项和,则
项和,则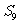 的值为( )
的值为( )
A、48 B、54 C、60 D、66
例1、(06广东)已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为( )
A、5 B、4 C、3 D、2
例2、(06上海春22)已知数列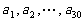 ,其中
,其中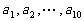 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;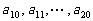 是公差为
是公差为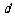 的等差数列;
的等差数列;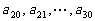 是公差为
是公差为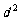 的等差数列(
的等差数列(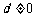 ).
).
(1)若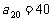 ,求
,求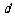 ;
;
(2)试写出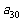 关于
关于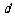 的关系式,并求
的关系式,并求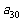 的取值范围;
的取值范围;
(3)续写已知数列,使得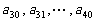 是公差为
是公差为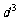 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
[解](1)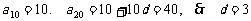 .
…… 4分
.
…… 4分
(2)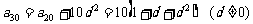 ,
…… 8分
,
…… 8分
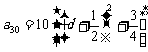 ,
,
当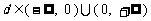 时,
时,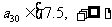 .
…… 12分
.
…… 12分
(3)所给数列可推广为无穷数列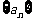 ,其中
,其中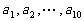 是首项为1,公差为1的等差数列,当
是首项为1,公差为1的等差数列,当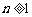 时,数列
时,数列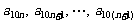 是公差为
是公差为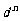 的等差数列.
…… 14分
的等差数列.
…… 14分
研究的问题可以是:试写出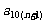 关于
关于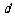 的关系式,并求
的关系式,并求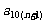 的取值范围.…… 16分
的取值范围.…… 16分
研究的结论可以是:由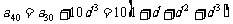 ,
,
依次类推可得 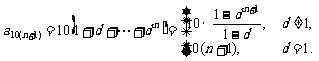
当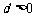 时,
时,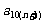 的取值范围为
的取值范围为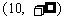 等.
…… 18分
等.
…… 18分
例3、(04天津20)设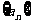 是一个公差为
是一个公差为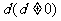 的等差数列,它的前10项和
的等差数列,它的前10项和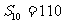 且
且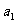 ,
,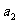 ,
, 成等比数列。(1)证明
成等比数列。(1)证明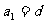 ;(2)求公差
;(2)求公差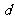 的值和数列
的值和数列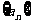 的通项公式。
的通项公式。
(三)解答题:
6、(07江苏20)已知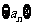 是等差数列,
是等差数列,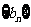 是公比为
是公比为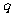 的等比数列,
的等比数列,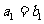 ,
,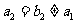 ,记
,记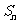 为数列
为数列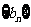 的前
的前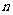 项和.
项和.
(1)若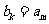 (
(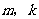 是大于
是大于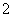 的正整数),求证:
的正整数),求证: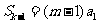 ;
;
(2)若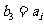 (
(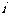 是某个正整数),求证:
是某个正整数),求证: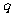 是整数,且数列
是整数,且数列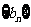 中的每一项都是数列
中的每一项都是数列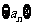 中的项;
中的项;
(3)是否存在这样的正数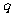 ,使等比数列
,使等比数列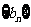 中有三项成等差数列?若存在,写出一个
中有三项成等差数列?若存在,写出一个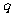 的值,并加以说明;若不存在,请说明理由.
的值,并加以说明;若不存在,请说明理由.
解:(1)设等差数列的公差为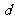 ,则由题设得
,则由题设得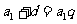 ,
,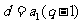 ,且
,且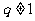 .
.
由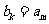 得
得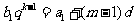 ,所以
,所以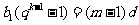 ,
,
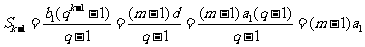 .
.
故等式成立.
(2)(ⅰ)证明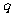 为整数:
为整数:
由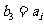 得
得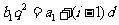 ,即
,即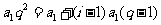 ,
,
移项得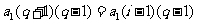 .
.
因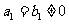 ,
,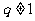 ,得
,得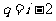 ,故
,故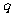 为整数.
为整数.
(ⅱ)证明数列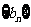 中的每一项都是数列
中的每一项都是数列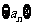 中的项:
中的项:
设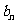 是数列
是数列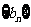 中的任一项,只要讨论
中的任一项,只要讨论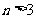 的情形.
的情形.
令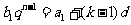 ,即
,即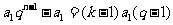 ,
,
得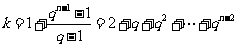 .
.
因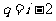 ,当
,当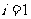 时,
时,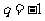 ,
,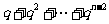 为
为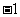 或
或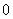 ,则
,则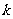 为
为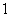 或
或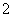 ;
;
而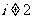 ,否则
,否则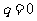 ,矛盾.
,矛盾.
当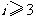 时,
时,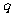 为正整数,所以
为正整数,所以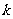 为正整数,从而
为正整数,从而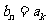 .
.
故数列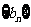 中的每一项都是数列
中的每一项都是数列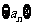 中的项.
中的项.
(3)取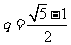 ,
,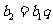 ,
,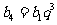 .
.
 .
.
所以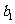 ,
,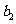 ,
,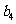 成等差数列。
成等差数列。
(二)填空题:
4、(07江西)已知数列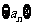 对于任意
对于任意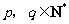 ,有
,有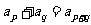 ,若
,若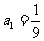 ,则
,则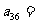 ;
;
5、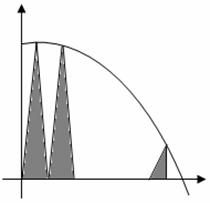 (07安徽)如图,抛物线
(07安徽)如图,抛物线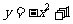 与
与 轴的正半轴交于点
轴的正半轴交于点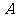 ,将线段
,将线段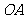 的
的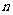 等分点从左至右依次记为
等分点从左至右依次记为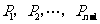 ,过这些分点分别作
,过这些分点分别作 轴的垂线,与抛物线的交点依次为
轴的垂线,与抛物线的交点依次为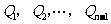 ,从而得到
,从而得到 个直角三角形
个直角三角形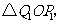
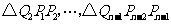 .当
.当 时,这些三角形
时,这些三角形
|
(一)选择题:
1、(05全国Ⅱ11)如果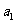 ,
,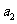 ,…,
,…,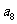 为各项都大于零的等差数列,公差
为各项都大于零的等差数列,公差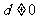 ,则
,则
A、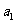
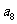
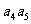 B、
B、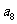
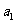
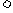
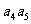 C、
C、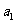 +
+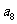
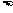
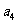 +
+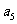 D、
D、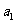
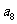 =
=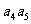
2、(04浙江)已知等差数列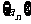 的公差为2,若
的公差为2,若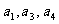 成等比数列, 则
成等比数列, 则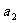 =( )
=( )
A、–4 B、–6 C、–8 D、–10
3、(04湖南11)农民收入由工资性收入和其它收入两部分构成 2003年某地区农民人均收入为3150元(其中工资性收入为1800元,其它收入为1350元), 预计该地区自2004年起的5 年内,农民的工资性收入将以每年6%的年增长率增长,其它收入每年增加160元根据以上数据,2008年该地区农民人均收入介于( )
2003年某地区农民人均收入为3150元(其中工资性收入为1800元,其它收入为1350元), 预计该地区自2004年起的5 年内,农民的工资性收入将以每年6%的年增长率增长,其它收入每年增加160元根据以上数据,2008年该地区农民人均收入介于( )
A、4200元~4400元 B、4400元~4600元 C、4600元~4800元 D、4800元~5000元
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com