
2. (07广东)已知函数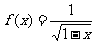 的定义域为
的定义域为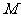 ,
,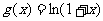 的定义域为
的定义域为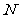 ,则
,则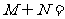 ( ) A.
( ) A.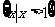 B.
B. C.
C.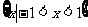 D.
D.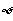
1. (2009广东)已知全集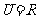 ,集合
,集合
和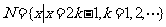 的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有( )
的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有( )
A. 3个 B. 2个 C. 1个 D. 无穷多个
(二)填空题:
8、(07山东)设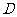 是不等式组
是不等式组 表示的平面区域,则
表示的平面区域,则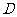 中的点
中的点 到直线
到直线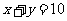 距离的最大值是
;
距离的最大值是
;
9、(06全国Ⅰ)设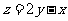 ,式中变量
,式中变量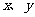 满足下列条件:
满足下列条件: 则
则 的最大值为_____________;
的最大值为_____________;
10、(07重庆)已知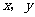 满足
满足 则函数
则函数 的最大值是______;
的最大值是______;
11、(07陕西)已知实数 满足条件
满足条件 则
则 的最大值为 ;
的最大值为 ;
12、(07湖北)设变量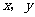 满足约束条件
满足约束条件 则目标函数
则目标函数 的最小值为 .
的最小值为 .
 (一)选择题:
(一)选择题:
1、(06广东)在约束条件 下,当
下,当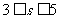 时,目标函数
时,目标函数 的最大值的变化范围是( )
的最大值的变化范围是( )
A、 B、
B、  C、
C、 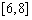 D、
D、 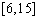
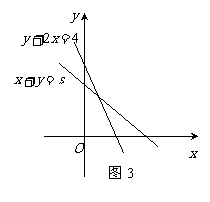
2、(06山东)某公司招收男职员x名,女职员y名, 须满足约束条件
须满足约束条件 则z=10x+10y的最大值是( )
则z=10x+10y的最大值是( )
A、80 B、 85 C、90 D、95
3、(04广东)变量 满足下列条件:
满足下列条件: ,则使
,则使 的值最小的
的值最小的 是( ) A、 ( 4.5 ,3 ) B、( 3,6 )
C、 ( 9, 2 ) D、( 6, 4 )
是( ) A、 ( 4.5 ,3 ) B、( 3,6 )
C、 ( 9, 2 ) D、( 6, 4 )
4、(07四川)某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙投资的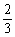 倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为( )
倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为( )
A、36万元 B、31.2万元 C、30.4万元 D、24万元
5、(07天津)设变量 满足约束条件
满足约束条件 则目标函数
则目标函数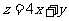 的最大值为( )
A、4 B、11 C、12 D、14
的最大值为( )
A、4 B、11 C、12 D、14
6、(07辽宁)已知变量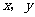 满足约束条件
满足约束条件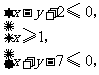 则
则 的取值范围是( )
的取值范围是( )
A、 B、
B、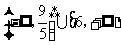 C、
C、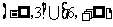 D、
D、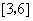
7、(07江苏)在平面直角坐标系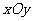 中,已知平面区域
中,已知平面区域
 ,则平面区域
,则平面区域 的面积为( )
的面积为( )
A、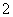 B、
B、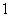 C、
C、 D、
D、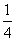
例1、(06湖南)已知 则
则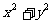 的最小值是_____________;
的最小值是_____________;
例2、(06重庆)已知变量 满足约束条件
满足约束条件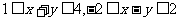 ,若目标函数
,若目标函数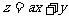 (其中
(其中 )仅在点(3,1)处取得最大值,则
)仅在点(3,1)处取得最大值,则 的取值范围为___________;
的取值范围为___________;
例3、(04江苏)制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损。某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和50﹪,可能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
(三)解答题:
7、(06全国Ⅰ)设数列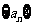 的前
的前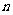 项的和
项的和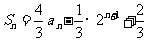 ,
,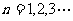
(Ⅰ)求首项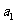 与通项
与通项 ;(Ⅱ)设
;(Ⅱ)设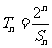 ,
,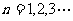 ,证明:
,证明: 。
。
解: (Ⅰ)由 Sn=an-×2n+1+, n=1,2,3,… , ① 得 a1=S1= a1-×4+ 所以a1=2.
再由①有 Sn-1=an-1-×2n+, n=2,3,4,…
将①和②相减得: an=Sn-Sn-1= (an-an-1)-×(2n+1-2n),n=2,3, …
整理得: an+2n=4(an-1+2n-1),n=2,3, … , 因而数列{ an+2n}是首项为a1+2=4,公比为4的等比数列,即 : an+2n=4×4n-1= 4n, n=1,2,3, …, 因而an=4n-2n, n=1,2,3, …,
(Ⅱ)将an=4n-2n代入①得 Sn= ×(4n-2n)-×2n+1 + = ×(2n+1-1)(2n+1-2)
= ×(2n+1-1)(2n-1)
Tn= = × = ×( - )
所以, 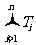 =
=  - ) = ×( - ) < 。
- ) = ×( - ) < 。
(二)填空题:
5、(07山东)函数
 的图象恒过定点
的图象恒过定点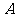 ,若点
,若点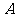 在直线
在直线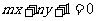 上,其中
上,其中 ,则
,则 的最小值为
;
的最小值为
;
6、(07上海)若 ,且
,且 ,则
,则 的最大值是
。
的最大值是
。
(一)选择题:
1、(07海南)已知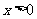 ,
, ,
,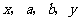 成等差数列,
成等差数列, 成等比数列,则
成等比数列,则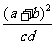 的最小值是( ) A、
的最小值是( ) A、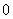 B、
B、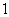 C、
C、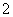 D、
D、
2、(07北京)如果正数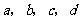 满足
满足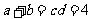 ,那么( )
,那么( )
A、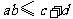 ,且等号成立时
,且等号成立时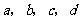 的取值唯一
的取值唯一
B、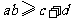 ,且等号成立时
,且等号成立时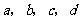 的取值唯一
的取值唯一
C、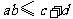 ,且等号成立时
,且等号成立时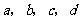 的取值不唯一
的取值不唯一
D、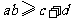 ,且等号成立时
,且等号成立时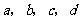 的取值不唯一
的取值不唯一
3、(06上海)若关于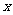 的不等式
的不等式 ≤
≤ +4的解集是
+4的解集是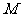 ,则对任意实常数
,则对任意实常数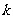 ,总有( )
,总有( )
A、2∈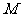 ,0∈
,0∈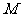 ; B、2
; B、2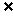
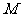 ,0
,0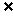
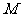 ;
;
C、2∈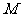 ,0
,0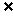
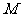 ; D、2
; D、2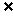
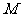 ,0∈
,0∈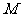
4、(06重庆)若 且
且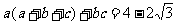 ,则
,则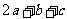 的最小值为( )
的最小值为( )
A、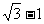 B、
B、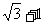 C、
C、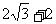 D、
D、
例1、(07上海春)设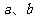 是正实数,以下不等式
是正实数,以下不等式
① 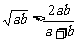 ,②
,② 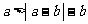 ,③
,③ 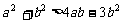 ,④
,④ 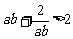
恒成立的序号为
(A) ①、③ (B) ①、④
(B) ①、④ (C) ②、③
(C) ②、③ (D) ②、④
(D) ②、④
例2、(05全国Ⅰ)当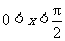 时,函数
时,函数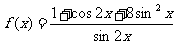 的最小值为( )
的最小值为( )
(A)2 (B) (C)4 (D)
(C)4 (D)
例3、(05全国Ⅲ)已知在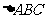 中,
中,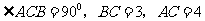 ,
,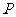 是
是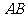 上的点,则点
上的点,则点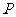 到
到 的距离乘积的最大值是
的距离乘积的最大值是
解:P到BC的距离为d1,P到AC的距离为d2,则三角形的面积得3d1+4d2=12,∴3d1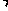 4d2≤
4d2≤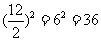 ,∴d1d2的最大值为3,这时3d1+4d2=12,
3d1=4d2得d1=2,d2=
,∴d1d2的最大值为3,这时3d1+4d2=12,
3d1=4d2得d1=2,d2=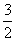 。
。
例4、(04吉林22)已知函数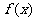
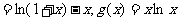 。(1)求函数
。(1)求函数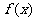 的最大值;(2)设
的最大值;(2)设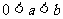 ,证明:
,证明: 。
。
(I)解:函数f(x)的定义域是(-1,∞),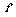 (x)=
(x)=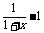 .令
.令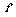 (x)=0,解得x=0,当-1<x<0时,
(x)=0,解得x=0,当-1<x<0时, 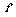 (x)>0,当x>0时,
(x)>0,当x>0时,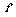 (x)<0,又f(0)=0,故当且仅当x=0时,f(x)取得最大值,最大值是0
(x)<0,又f(0)=0,故当且仅当x=0时,f(x)取得最大值,最大值是0
(II)证法一:g(a)+g(b)-2g(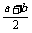 )=alna+blnb-(a+b)ln
)=alna+blnb-(a+b)ln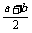 =a
=a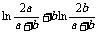 .
.
由(I)的结论知ln(1+x)-x<0(x>-1,且x≠0),由题设0<a<b,得 ,因此
,因此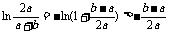 ,
,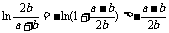 .
.
所以a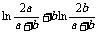 >-
>-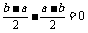 .
.
又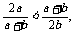 a
a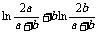 <a
<a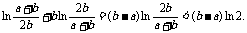
综上0<g(a)+g(b)-2g(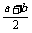 )<(b-a)ln2.
)<(b-a)ln2.
(II)证法二:g(x)=xlnx,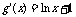 ,设F(x)= g(a)+g(x)-2g(
,设F(x)= g(a)+g(x)-2g(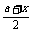 ),
),
则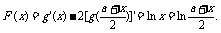 当0<x<a时
当0<x<a时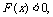 因此F(x)在(0,a)内为减函数
因此F(x)在(0,a)内为减函数 当x>a时
当x>a时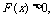 因此F(x)在(a,+∞)上为增函数
因此F(x)在(a,+∞)上为增函数 从而,当x=a时,F(x)有极小值F(a)
从而,当x=a时,F(x)有极小值F(a) 因为F(a)=0,b>a,所以F(b)>0,即0<g(a)+g(b)-2g(
因为F(a)=0,b>a,所以F(b)>0,即0<g(a)+g(b)-2g(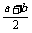 ).
).
设G(x)=F(x)-(x-a)ln2,则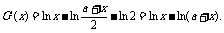 当x>0时,
当x>0时,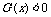 ,因此G(x)在(0,+∞)上为减函数,因为G(a)=0,b>a,所以G(b)<0.即g(a)+g(b)-2g(
,因此G(x)在(0,+∞)上为减函数,因为G(a)=0,b>a,所以G(b)<0.即g(a)+g(b)-2g(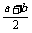 )<(b-a)ln2.
)<(b-a)ln2.
(三)解答题:
4、(06四川22)已知函数 ,
,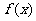 的导函数是
的导函数是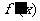 。对任意两个不相等的正数
。对任意两个不相等的正数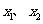 ,证明:
,证明:
(Ⅰ)当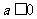 时,
时,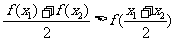 ;
;
(Ⅱ)当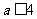 时,
时,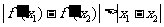 。
。
证明:(Ⅰ)由
得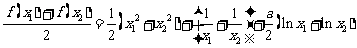

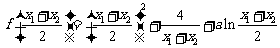
而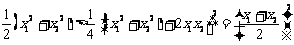 ①
①
又
∴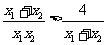 ②
②
∵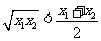 ∴
∴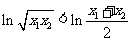
∵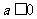 ∴
∴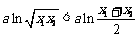 ③
③
由①、②、③得
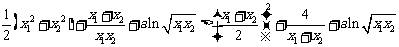
即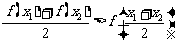
(Ⅱ)证法一:由 ,得
,得
∴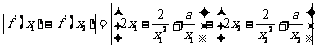
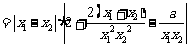

下面证明对任意两个不相等的正数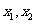 ,有
,有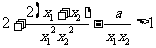 恒成立
恒成立
即证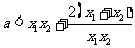 成立
成立
∵
设 ,则
,则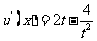
令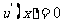 得
得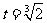 ,列表如下:
,列表如下:
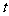 |
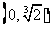 |
 |
 |
 |
 |
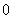 |
 |
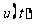 |
 |
极小值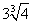 |
 |
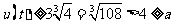 ∴
∴
∴对任意两个不相等的正数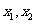 ,恒有
,恒有
证法二:由 ,得
,得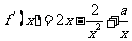
∴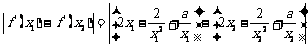
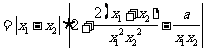
∵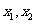 是两个不相等的正数
是两个不相等的正数
∴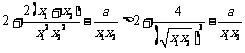

设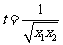 ,
,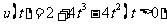
则 ,列表:
,列表:
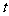 |
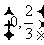 |
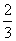 |
 |
 |
 |
 |
 |
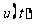 |
 |
极小值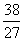 |
 |
∴ 即
即 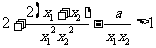
∴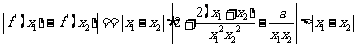
即对任意两个不相等的正数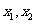 ,恒有
,恒有
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com