
6.(2010辽宁沈阳一摸)
在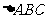 中,A、B、C为三角形的三个内角,且满足条件
中,A、B、C为三角形的三个内角,且满足条件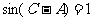 ,
,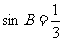 .
.
(Ⅰ)求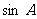 的值;
的值;
(Ⅱ)若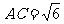 ,求
,求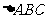 的面积.
的面积.
5.(2010北京宣武模拟题)
已知函数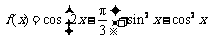
⑴求函数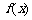 的最小正周期及图象的对称轴方程;
的最小正周期及图象的对称轴方程;
⑵设函数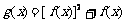 ,求
,求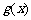 的值域.
的值域.
4.(2010陕西省高三冲刺卷)
已知函数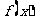 为定义在R上的奇函数,且当
为定义在R上的奇函数,且当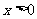 时,
时,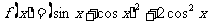 ,
,
(1) 求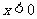 时
时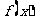 的表达式;
的表达式;
(2) 若关于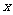 的方程
的方程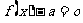 有解,求实数
有解,求实数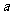 的范围。
的范围。
3.(2010山东济宁五中5月模拟)
在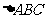 中,
中,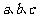 分别为角
分别为角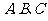 的对边,且满足
的对边,且满足 。
。
(Ⅰ)求角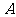 的值;
的值;
(Ⅱ)若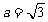 ,设角
,设角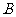 的大小为
的大小为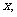
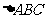 的周长为
的周长为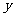 ,求
,求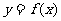 的最大值。
的最大值。
2.(2010英才苑模拟、辽宁丹东2009-2010学年度下高一期末质量监测)
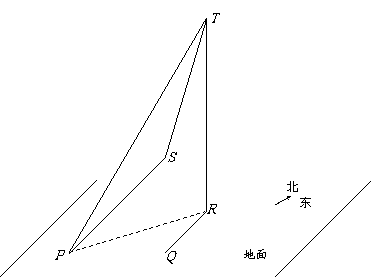 一气球以V(m/s)的速度由地面上升,10分钟后由观察点P测得气球在P的正东方向S处,仰角为
一气球以V(m/s)的速度由地面上升,10分钟后由观察点P测得气球在P的正东方向S处,仰角为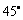 ;再过10分钟后,测得气球在P的东偏北
;再过10分钟后,测得气球在P的东偏北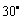 方向T处,其仰角为
方向T处,其仰角为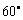 (如图,其中Q、R分别为气球在S、T处时的正投影).求风向和风速(风速用V表示).
(如图,其中Q、R分别为气球在S、T处时的正投影).求风向和风速(风速用V表示).
1.(2010北京朝阳区模拟)
在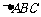 中,角
中,角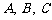 所对的边分别为
所对的边分别为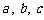 ,且
,且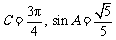 .
.
⑴求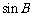 的值;
的值;
⑵若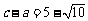 ,求
,求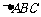 的面积.
的面积.
10.

9. 解:(I)当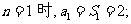 ………………(2分)
………………(2分)
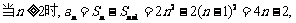
故{an}的通项公式为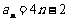 ;
………………(4分)
;
………………(4分)
设{bn}的通项公式为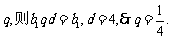
故 ………………(6分)
………………(6分)
(II) ………………(8分)
………………(8分)
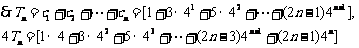
两式相减得 ………………(10分)
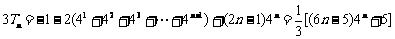
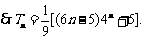 ………………(12分)
………………(12分)
8. 解:(1)证法一:当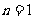 时,
时,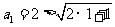 ,不等式成立,
,不等式成立,
假设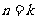 时,
时,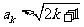 成立 (2分),
成立 (2分),
当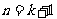 时,
时,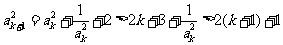 .(5分)
.(5分)
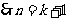 时,
时,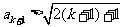 时成立
时成立
综上由数学归纳法可知, 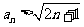 对一切正整数成立 (6分)
对一切正整数成立 (6分)
证法二:当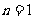 时,
时,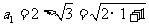 ,结论成立;
,结论成立;
假设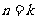 时结论成立,即
时结论成立,即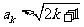 (2分) 当
(2分) 当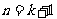 时,
时,
由函数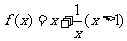 的单增性和归纳假设有
的单增性和归纳假设有
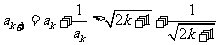 (4分),
(4分),
因此只需证: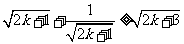 ,
,
而这等价于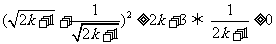 ,
,
显然成立,所以当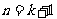 是,结论成立;
是,结论成立;
综上由数学归纳法可知, 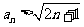 对一切正整数成立 (6分)
对一切正整数成立 (6分)
证法三:由递推公式得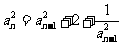 ,
,
 (2分)
(2分)
上述各式相加并化简得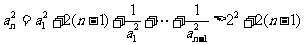
 (4分)
(4分)
又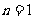 时,
时,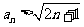 显然成立, 故
显然成立, 故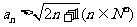 (6分)
(6分)
7. ⑴∵点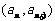 在直线
在直线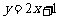 上,∴
上,∴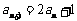
∴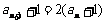 ,
,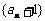 是以
是以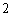 为首项,
为首项,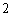 为公比的等比数列,
为公比的等比数列,
∴
⑵∵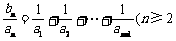 且
且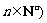 ,
,
∴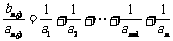 ,
,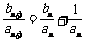
∴ 且
且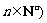 ;
;
当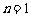 时,
时,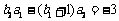 .
.
⑶由⑵知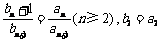
∴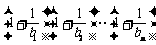

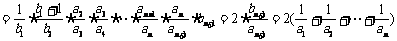
∵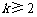 时,
时,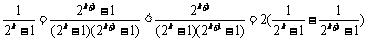
∴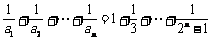
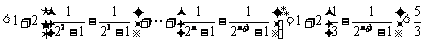 ,
,
∴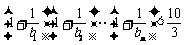 ,
,
即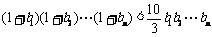 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com